Câu hỏi:
2 năm trước
Cho hình thang cân \(MNPQ\) (\(MN\) //\(PQ\)) có góc \(\widehat {MQP} = {45^0}\) và hai đáy có độ dài \(8cm\), \(30cm\). Diện tích của hình thang cân là:
Trả lời bởi giáo viên
Đáp án đúng: b
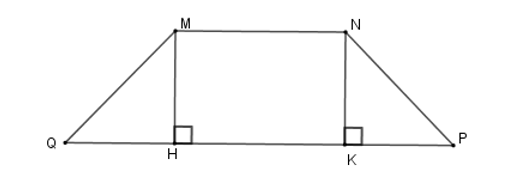
Kẻ \(MH \bot QP;\,NK \bot QP\) tại \(H,\,K \Rightarrow MH{\rm{//}}NK\).
Tứ giác \(MNHK\) có: \(MN{\rm{//}}HK\) nên \(MNHK\) là hình thang, lại có \(MH{\rm{//}}NK \Rightarrow MN = HK;\,MH = NK\).
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có: \(MQ = NP\) (vì \(MNPQ\) là hình thang cân) suy ra \(\Delta MQH = \Delta NKP\,\left( {ch - cgv} \right)\)\( \Rightarrow QH = KP = \dfrac{{QP - HK}}{2}\)
Mà \(HK = MN = 8\,cm\) nên \(QH = KP = \dfrac{{30 - 8}}{2} = 11\,cm\).
Mà \(\widehat {MQP} = 45^\circ \Rightarrow \Delta MHQ\) vuông cân tại \(H \Rightarrow MH = QH = 11\,cm\).
Diện tích hình thang cân \(MNPQ\) là \({S_{MNPQ}} = \dfrac{{\left( {MN + PQ} \right).MH}}{2} = \dfrac{{\left( {8 + 30} \right).11}}{2} = 209\,c{m^2}\).
Hướng dẫn giải:
Bước 1: Kẻ các đường cao \(MH,\,NK\). Sử dụng tính chất về cạnh của hình thang cân để tính chiều cao hình thang.
Bước 2: Áp dụng công thức diện tích \({S_{MNPQ}} = \dfrac{{\left( {MN + PQ} \right).MH}}{2}\).
