Câu hỏi:
2 năm trước
Cho hình thang cân \(ABCD\) đáy nhỏ \(AB = 12cm\), đáy lớn \(CD = 22cm\), cạnh bên \(BC = 13cm\) thì đường cao \(AH\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
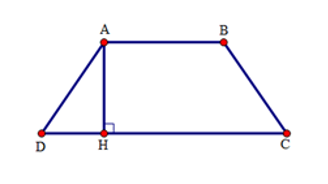
Ta có: \(DH = \dfrac{1}{2}\left( {CD - AB} \right) = \dfrac{1}{2}\left( {22 - 12} \right) = 5\,\,cm\).
Do \(ABCD\) là hình thang cân nên \(AD = BC = 13cm\).
Áp dụng định lý Py– ta – go vào tam giác \(ADH\) vuông tại \(H\), ta có: \(A{D^2} = A{H^2} + D{H^2}\).
\( \Rightarrow A{H^2} = A{D^2} - D{H^2} = {13^2} - {5^2} \Rightarrow AH = 12\).
Vậy \(AH = 12cm\) .

