Cho hình thang cân \(ABCD\) (\(AB\) //\(CD\)) có hai đường chéo cắt nhau tại \(I\), hai đường thẳng \(AD\) và \(BC\) cắt nhau ở \(K\). Chọn câu sai.

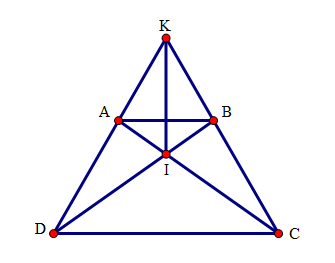
* Xét tam giác \(ACD\) và tam giác \(BDC\) có:

+ \(AD = BC\) (do \(ABCD\) là hình thang cân)

+ \(AC = BD\) (do \(ABCD\) là hình thang cân)

+ \(CD\) là cạnh chung

Suy ra \(\Delta ACD = \Delta BDC\) (c.c.c). Suy ra \(\widehat {ACD} = \widehat {BDC}\) (hai góc tương ứng).

Xét tam giác \(ICD\) có \(\widehat {ACD} = \widehat {BDC}\) (cmt), suy ra tam giác \(ICD\) cân tại\(I\).

Nên C sai vì ta chưa đủ điều kiện để \(IC = CD.\)

Tam giác \(KCD\) có hai góc ở đáy bằng nhau nên tam giác \(KCD\) cân ở \(K\) nên B đúng.

* Xét tam giác \(KDI\) và tam giác \(KCI\) có:

+ \(KD = KC\) (do \(\Delta KCD\) cân tại \(K\))

+ \(KI\) là cạnh chung

+ \(IC = ID\) (do \(\Delta ICD\) cân tại \(I\))

Suy ra \(\Delta KDI = \Delta KCI\) (c.c.c). Suy ra \(\widehat {DKI} = \widehat {CKI}\), do đó \(KI\) là phân giác \(\widehat {AKB}\) nên D đúng.

Ta có: \(AB//CD\) (do \(ABCD\) là hình thang) nên \(\widehat {KAB} = \widehat {KCD};\,\widehat {KBA} = \widehat {KCD}\) (các cặp góc đồng vị bằng nhau)

Mà \(\widehat {KDC} = \widehat {KCD}\) (tính chất hình thang cân) nên \(\widehat {KAB} = \widehat {KBA}\) hay \(\Delta {\rm K}{\rm A}{\rm B}\) cân tại \(K\). Do đó A đúng.