Câu hỏi:
2 năm trước
Cho hình thang \(ABCD\) có: \(AB//CD\), \(AB = 4,CD = 16,\)\(AC = 8,AD = 12\). Độ dài \(BC\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
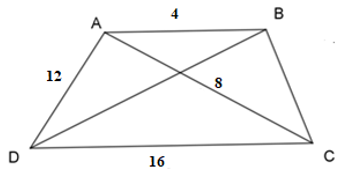
Ta có:
\(\dfrac{{AB}}{{AC}} = \dfrac{4}{8} = \dfrac{1}{2}\), \(\dfrac{{AC}}{{CD}} = \dfrac{8}{{16}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{CD}} = \dfrac{1}{2}\)
Xét \(\Delta ABC\) và \(\Delta CAD\) có:
\(\dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{CD}}\) (chứng minh trên)
\(\widehat {BAC} = \widehat {ACD}\) (cặp góc so le trong)
\( \Rightarrow \Delta ABC\backsim\Delta CAD\) (c – g – c)
\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{CA}}{{CD}} = \dfrac{{BC}}{{AD}} = \dfrac{1}{2}\)\( \Rightarrow \dfrac{{BC}}{{12}} = \dfrac{1}{2} \Rightarrow x = \dfrac{{12.1}}{2} = 6\).
Hướng dẫn giải:
- Xét tỉ số độ dài của các cạnh tương ứng của 2 tam giác.
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
- Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị của x.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
