Câu hỏi:
2 năm trước
Cho hình thang \(ABCD\) có \(\widehat A = \widehat D = {90^0},\widehat B = {60^0},CD = 30cm,CA \bot CB\). Tính diện tích của hình thang.
Trả lời bởi giáo viên
Đáp án đúng: a
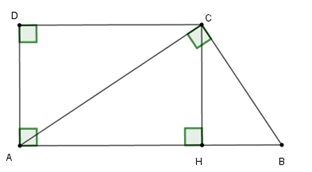
Ta có $\tan \widehat{CAD}=\dfrac{DC}{AD}\Leftrightarrow AD=DC:\tan 60^0=AD = 10\sqrt 3$ \(\left( {cm} \right)\).
Kẻ \(CH \bot AB\). Tứ giác \(AHCD\) là hình chữ nhật vì có \(\widehat A = \widehat D = \widehat H = {90^0}\), suy ra \(AH = CD = 30cm;CH = AD = 10\sqrt 3 \left( {cm} \right)\).
Tam giác \(ACB\) vuông tại \(C\), ta có: \(C{H^2} = HA.HB\), suy ra \(HB = \dfrac{{C{H^2}}}{{HA}} = \dfrac{{{{\left( {10\sqrt 3 } \right)}^2}}}{{30}} = \dfrac{{300}}{{30}} = 10\left( {cm} \right)\),
do đó \(AB = AH + HB = 30 + 10 = 40\left( {cm} \right).\)
\({S_{ABCD}} = \dfrac{1}{2}CH\left( {AB + CD} \right)=\dfrac{1}{2}.10\sqrt 3 .\left( {40 + 30} \right) = 350\sqrt 3 \left( {c{m^2}} \right).\)
Vậy diện tích hình thang \(ABCD\) bằng \(350\sqrt 3 c{m^2}\)
Hướng dẫn giải:
Kẻ \(CH \bot AB\).
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông
