Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.A'B'C'D'\). Đường thẳng \(AC'\) vuông góc với mặt phẳng nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: a
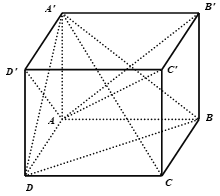
Ta có:
$\left\{ {\begin{array}{*{20}{c}}{A'D \bot AD'{\rm{ }}\left( \text{t/c hình vuông} \right)}\\{A'D \bot C'D'{\rm{ }}\left( {C'D' \bot \left( {A'D'DA} \right)} \right)}\end{array}} \right.$
$ \Rightarrow A'D \bot \left( {AC'D'} \right) \Rightarrow A'D \bot AC'{\rm{ }}\left( 1 \right)$
$\left\{ {\begin{array}{*{20}{c}}{A'B \bot AB'{\rm{ }}\left( \text{t/c hình vuông} \right)}\\{A'B \bot B'C'{\rm{ }}\left( {B'C' \bot \left( {A'D'DA} \right)} \right)}\end{array}} \right.$
$ \Rightarrow A'B \bot \left( {AB'C'} \right) \Rightarrow A'B \bot AC'{\rm{ }}\left( 2 \right)$
Từ $\left( 1 \right),\left( 2 \right) \Rightarrow AC' \bot \left( {A'BD} \right)$
Hướng dẫn giải:
Sử dụng tính chất \(\left\{ \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot b\)
