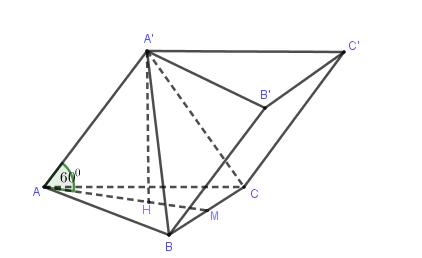
Cho hình lăng trụ tam giác $ABC.A'B'C'$ có các cạnh bên hợp với đáy những góc bằng $60^\circ$, đáy $ABC$ là tam giác đều cạnh $a$ và $A'$ cách đều $A$, $B$, $C$. Tính khoảng cách giữa hai đáy của hình lăng trụ.

Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ song song với nhau và một điểm $M$ không thuộc $\left( P \right)$ và $\left( Q \right)$. Qua $M$ có bao nhiêu mặt phẳng vuông góc với $\left( P \right)$ và $\left( Q \right)$?

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B$ và cạnh bên $SB$ vuông góc với mặt phẳng đáy. Cho biết $SB = 3a$, $AB = 4a$, $BC = 2a$. Tính khoảng cách từ $B$ đến mặt phẳng $\left( {SAC} \right).$

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $SA \bot \left( {ABC} \right)$,$SA = a$. Gọi $\left( P \right)$ là mặt phẳng đi qua $S$ và vuông góc với $BC$. Thiết diện của $\left( P \right)$ và hình chóp $S.ABC$ có diện tích bằng ?

Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ không đồng phẳng xét các vectơ $\overrightarrow x  = 2\overrightarrow a  - \overrightarrow b ;\overrightarrow y  =  - 4\overrightarrow a  + 2\overrightarrow b ;$ $\overrightarrow z  =  - 3\overrightarrow a  - 2\overrightarrow c$

Chọn mệnh đề đúng trong các mệnh đề sau:

Cho tứ diện $ABCD$ có $AB,AC,AD$ đôi một vuông góc. Chỉ ra mệnh đề sai trong các mệnh đề sau:

Cho hình chóp $S.ABC$ trong đó $SA,{\rm{ }}AB,{\rm{ }}BC$ đôi một vuông góc và $SA = AB = BC = 1.$ Khoảng cách giữa hai điểm $S$ và $C$ nhận giá trị nào trong các giá trị sau ?

Cho hình chóp $S.ABC$ có đáy $ABCD$ là hình vuông cạnh $a,$ tâm $O.$ Cạnh bên $SA = 2a$ và vuông góc với mặt đáy $(ABCD).$ Gọi $H$ và $K$ lần lượt là trung điểm của cạnh $BC$ và $CD.$ Tính khoảng cách giữa hai đường thẳng $HK$ và $SD.$