Câu hỏi:
2 năm trước
Cho hình lăng trụ đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thang vuông \(\left( {\widehat A = \widehat B = {{90}^0}} \right)\) .
Có bao nhiêu cạnh vuông góc với mặt phẳng \(\left( {BCC'B'} \right)\) ?
Trả lời bởi giáo viên
Đáp án đúng: b
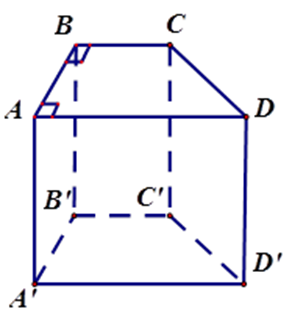
Vì \(AB \bot BC\) (do \(ABCD\) là hình thang vuông) và \(AB \bot BB'\) (tính chất lăng trụ đứng)
Nên \(AB \bot \left( {BCC'B'} \right)\) , tương tự ta có \(A'B' \bot \left( {BCC'B'} \right)\)
Do đó $AB,A'B'$ vuông góc với mp $\left( {BCC'B'} \right).$
Hướng dẫn giải:
Sử dụng quan hệ vuông góc giữa đường thẳng và mặt phẳng.