Cho hình lăng trụ đều \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có độ dài tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm A B và \(N\) là điểm thuộc cạnh A C sao cho \(CN = 2AN\). Thể tích của khối đa diện lồi có các đỉnh là các điểm \(A,M,N,{A^\prime },{B^\prime }\) và \({C^\prime }\) bằng

Cách 1

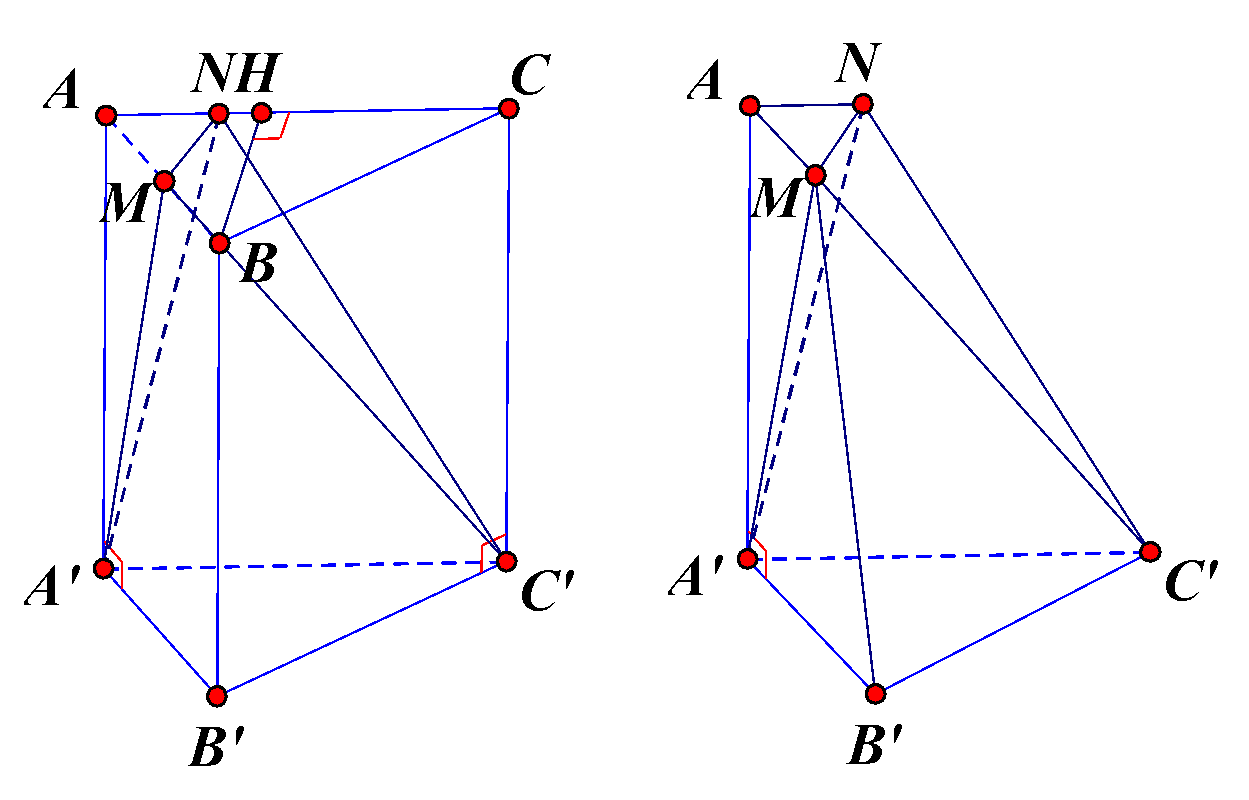
Gọi \(V\) là thể tích của của khối đa diện lồi có các đỉnh là các điểm \(A,M,N,{A^\prime },{B^\prime }\) và \({C^\prime }\). Khi đó ta có \(V = {V_{M \cdot {A^\prime }AN}} + {V_{M \cdot {A^\prime }{C^\prime }N}} + {V_{M \cdot {A^\prime }{B^\prime }{C^\prime }}}\).

Từ giả thiết ta có

\({S_{\Delta {A^\prime }AN}} = \dfrac{1}{2}A{A^\prime } \cdot AN = \dfrac{1}{2} \cdot a \cdot \dfrac{a}{3} = \dfrac{{{a^2}}}{6};{S_{\Delta {A^\prime }{C^\prime }N}} = \dfrac{1}{2}d\left( {N,{A^\prime }{C^\prime }} \right) \cdot {A^\prime }{C^\prime } = \dfrac{1}{2} \cdot a \cdot a = \dfrac{{{a^2}}}{2};\)

\({S_{\Delta {A' }{B' }{C'}}} = \dfrac{1}{2}{A' }{B' } \cdot {A' }{C' } \cdot \sin {60^0 } = \dfrac{{{a^2}\sqrt 3 }}{4}.\)

Gọi \(H\) là trung điểm của \(AC \Rightarrow BH \bot \left( {AC{C^\prime }{A^\prime }} \right)\) và \(BH = \dfrac{{a\sqrt 3 }}{2}\)

\( \Rightarrow d\left( {M,\left( {AC{C^\prime }{A^\prime }} \right)} \right) = \dfrac{1}{2}d\left( {B,\left( {AC{C^\prime }{A^\prime }} \right)} \right)\)\( = \dfrac{1}{2}BH = \dfrac{{a\sqrt 3 }}{4}\)

Khi đó ta có

\({V_{M \cdot {A^\prime }AN}} = \dfrac{1}{3}d\left( {M,\left( {AC{C^\prime }{A^\prime }} \right)} \right) \cdot {S_{\Delta {A^\prime }AN}}\)\( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt 3 }}{4} \cdot \dfrac{{{a^2}}}{6} = \dfrac{{{a^3}\sqrt 3 }}{{72}}\)\({V_{M \cdot {A^\prime }{B^\prime }{C^\prime }}} = \dfrac{1}{3}d\left( {M,\left( {{A^\prime }{B^\prime }{C^\prime }} \right)} \right) \cdot {S_{\Delta {A^\prime }{B^\prime }{C^\prime }}}\)\( = \dfrac{1}{3} \cdot a \cdot \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)

\({V_{M \cdot {A^\prime }{C^\prime }N}}\)\( = \dfrac{1}{3}d\left( {M,\left( {AC{C^\prime }{A^\prime }} \right)} \right) \cdot {S_{\Delta {A^\prime }{C^\prime }N}}\)\( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt 3 }}{4} \cdot \dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\)

Vậy

\(V = {V_{M \cdot {A^\prime }AN}} + {V_{M \cdot {A^\prime }{C^\prime }N}} + {V_{M \cdot {A^\prime }{B^\prime }{C^\prime }}}\)\( = \dfrac{{{a^3}\sqrt 3 }}{{72}} + \dfrac{{{a^3}\sqrt 3 }}{{24}} + \dfrac{{{a^3}\sqrt 3 }}{{12}} = \dfrac{{5\sqrt 3 {a^3}}}{{36}}\)

Cách 2:

Gọi \(V\) là thể tích của của khối đa diện lồi có các đỉnh là các điểm \(A,M,N,{A^\prime },{B^\prime }\) và \({C^\prime }\). Khi đó ta có \(V = {V_M} \cdot A{A^\prime }{C^\prime }N + {V_{M.{A^\prime }{B^\prime }{C^\prime }}}\).

Ta có \({S_{A{A^\prime }{C^\prime }N}} = \dfrac{1}{2}A{A^\prime }\left( {AN + {A^\prime }{C^\prime }} \right) = \dfrac{1}{2}a\left( {\dfrac{a}{3} + a} \right) = \dfrac{{2{a^2}}}{3}\).

Suy ra \({V_{M \cdot A{A^\prime }{C^\prime }N}} = \dfrac{1}{3}d\left( {M,\left( {AC{C^\prime }{A^\prime }} \right)} \right) \cdot {S_{A{A^\prime }{C^\prime }N}}\)\( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt 3 }}{4} \cdot \dfrac{{2{a^3}}}{3} = \dfrac{{2\sqrt 3 {a^3}}}{{36}}\)

\({V_{M \cdot {A^\prime }{B^\prime }{C^\prime }}} = \dfrac{1}{3}d\left( {M,\left( {{A^\prime }{B^\prime }{C^\prime }} \right)} \right).{S_{\Delta {A^\prime }{B^\prime }{C^\prime }}}\)\( = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)

Vậy \(V = {V_{M \cdot A{A^\prime }{C^\prime }N}} + {V_{M \cdot {A^\prime }{B^\prime }{C^\prime }}}\)\( = \dfrac{{2\sqrt 3 {a^3}}}{{36}} + \dfrac{{{a^3}\sqrt 3 }}{{12}} = \dfrac{{5\sqrt 3 {a^3}}}{{36}}\)

Cách 3:

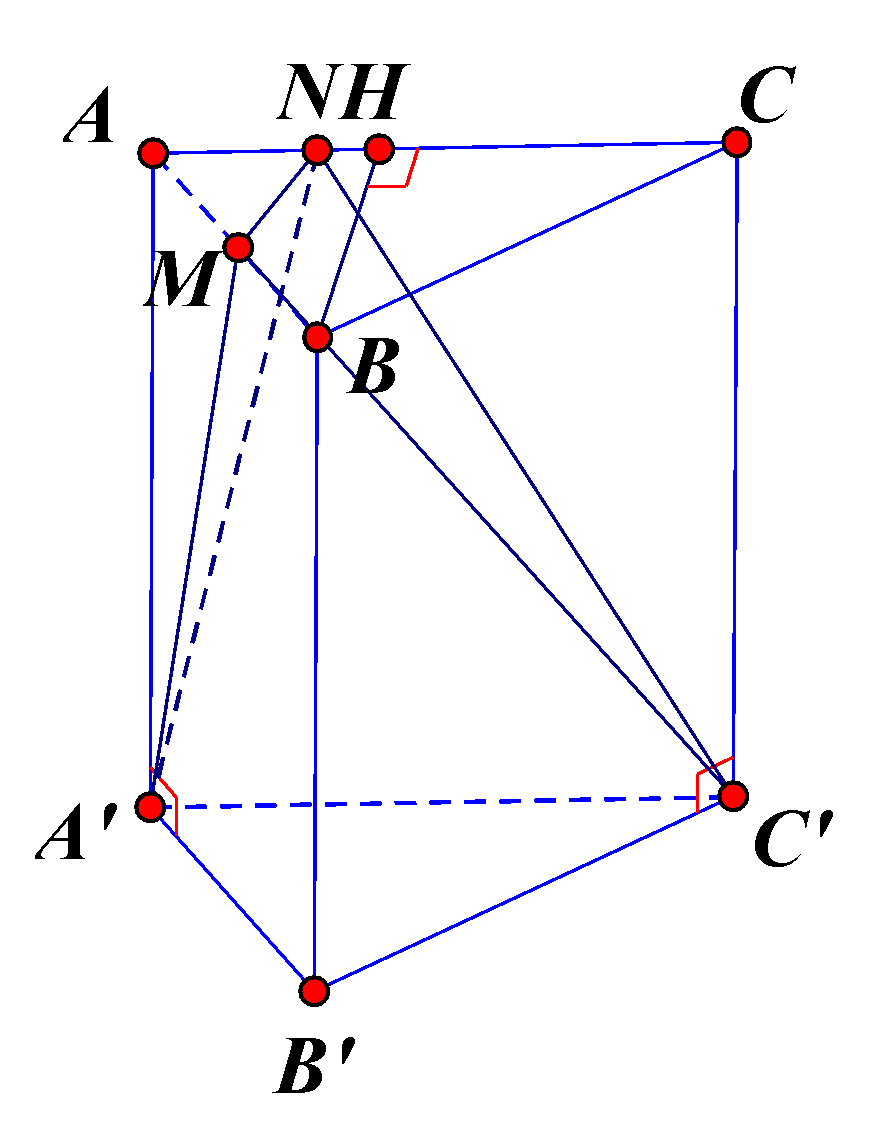
Gọi \(H\) là trung điểm của AC và \(V\) là thể tích của của khối đa diện lồi có các đỉnh là các điểm \(A,M,N,{A^\prime },{B^\prime }\) và \({C^\prime }\). Khi đó, \(V = {V_{AMH \cdot {A^\prime }{B^\prime }{C^\prime }}} - {V_{M \cdot NH{C^\prime }}}\).

Dễ thấy \(MH//{B^\prime }{C^\prime }\) nên \(AMH \cdot {A^\prime }{B^\prime }{C^\prime }\) là khối chóp cụt.

Áp dụng công thức thể tích \({V_1}\) của khối chóp cụt có chiều cao \(h\), diện tích đáy nhỏ và đáy lớn theo thứ tự là \({S_0},{S_1}\) thì ta có \({V_1} = \dfrac{h}{3}\left( {{S_0} + \sqrt {{S_0}{S_1}}  + {S_1}} \right)\).

Khi đó

\({V_{AMH \cdot {A^\prime }{B^\prime }{C^\prime }}} = \dfrac{{A{A^\prime }}}{3}\left( {{S_{AMH}} + \sqrt {{S_{AMH}} \cdot {S_{{A^\prime }{B^\prime }{C^\prime }}}}  + {S_{{A^\prime }{B^\prime }{C^\prime }}}} \right)\)

\( = \dfrac{a}{3}\left( {\dfrac{1}{4} \cdot \dfrac{{{a^2}\sqrt 3 }}{4} + \sqrt {\dfrac{1}{4} \cdot \dfrac{{{a^2}\sqrt 3 }}{4} \cdot \dfrac{{{a^2}\sqrt 3 }}{4}}  + \dfrac{{{a^2}\sqrt 3 }}{4}} \right)\)\( = \dfrac{{7{a^3}\sqrt 3 }}{{48}}\)

Mặt khác, \({V_{M \cdot NH{C^\prime }}} = \dfrac{1}{3}d\left( {M,\left( {AC{C^\prime }{A^\prime }} \right)} \right) \cdot {S_{NH{C^\prime }}}\)\( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt 3 }}{4} \cdot \dfrac{1}{2} \cdot a \cdot \dfrac{a}{6} = \dfrac{{{a^3}\sqrt 3 }}{{144}}\).

Vậy \(V = {V_{AMH \cdot {A^\prime }{B^\prime }{C^\prime }}} - {V_{M \cdot NH{C^\prime }}}\)\( = \dfrac{{7{a^3}\sqrt 3 }}{{48}} - \dfrac{{{a^3}\sqrt 3 }}{{144}} = \dfrac{{5\sqrt 3 {a^3}}}{{36}}\).