Cho hình hộp \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi cạnh $a\sqrt 3 ,{\mkern 1mu} BD = 3a,$ hình chiếu vuông góc của \(B\) trên mặt phẳng $\left( {A'B'C'D'} \right)$ trùng với trung điểm của \(A’C’\). Gọi $\alpha $ là góc tạo bởi hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {CDD'C'} \right), \cos \alpha  = \dfrac{{\sqrt {21} }}{7}$ . Thể tích của khối hộp \(ABCD.A’B’C’D\) bằng

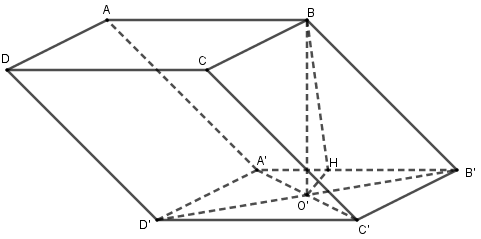
Gọi \(O'\) là trung điểm của \(A'C'\) ta có \(BO' \bot \left( {A'B'C'D'} \right)\)

Dễ thấy \(\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\) và \(\left( {CDD'C'} \right)//\left( {ABB'A'} \right)\) nên góc giữa hai mặt phẳng \(\left( {CDD'C'} \right)\) và \(\left( {ABCD} \right)\) bằng góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'D'} \right)\).

Xét tam giác \(ABD\) có :

\(\cos \widehat {BAD} = \dfrac{{A{B^2} + A{D^2} - B{D^2}}}{{2.AB.AD}}\)\( = \dfrac{{3{a^2} + 3{a^2} - 9{a^2}}}{{2.a\sqrt 3 .a\sqrt 3 }} =  - \dfrac{1}{2}\)

\( \Leftrightarrow \widehat {BAD} = {120^0}\) \( \Rightarrow \widehat {ADC} = {60^0}\)

\( \Rightarrow \Delta ACD\) đều, do đó \( \Rightarrow \Delta A'C'D'\) đều cạnh \(a\sqrt 3 \)

\( \Rightarrow {S_{A'C'D'}} = \dfrac{{{{\left( {a\sqrt 3 } \right)}^2}\sqrt 3 }}{4} = \dfrac{{3{a^2}\sqrt 3 }}{4}\) \( \Rightarrow {S_{A'B'C'D'}} = 2{S_{A'C'D'}} = \dfrac{{3{a^2}\sqrt 3 }}{2}\)

Kẻ \(O'H \bot A'B'\) thì \(A'B' \bot \left( {BO'H} \right)\) \( \Rightarrow A'B' \bot BH\).

Suy ra góc giữa \(\left( {A'B'C'D'} \right)\) và \(\left( {A'B'BA} \right)\) bằng \(\widehat {\left( {BH,O'H} \right)} = \widehat {BHO'} = \alpha \)

Mà \(\cos \alpha  = \dfrac{{\sqrt {21} }}{7}\) nên \(\tan \alpha  = \dfrac{2}{{\sqrt 3 }}\) \( \Rightarrow BO' = O'H\tan \alpha  = \dfrac{{2O'H}}{{\sqrt 3 }}\)

Lại có \(O'H = A'O'\sin {60^0} = \dfrac{{A'C'}}{2}.\sin {60^0}\) \( = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{4}\) \( \Rightarrow BO' = \dfrac{{2.\dfrac{{3a}}{4}}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{2}\).

Vậy \({V_{ABCD.A'B'C'D'}} = {S_{A'B'C'D'}}.BO'\) \( = \dfrac{{3{a^2}\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{9{a^3}}}{4}\)