Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh $2a$ và . Biết góc giữa đường thẳng $SA$ và mặt đáy bằng \({45^o}\). Thể tích khối chóp $S.ABC$ bằng

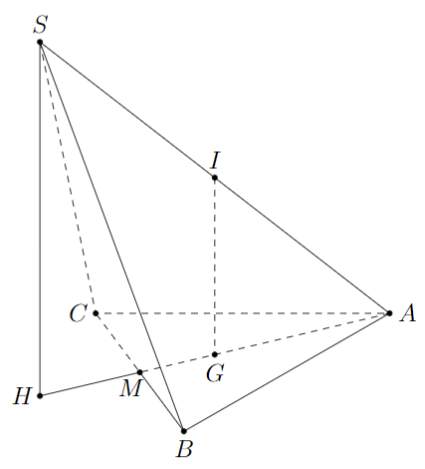
Gọi I là trung điểm của $S A$.

Tam giác $S A B$ và $S A C$ là các tam giác vuông tại \(B,C \Rightarrow IS = IA = IB = IC\).

Gọi \(G\) là trọng tâm tam giác đều \(ABC \Rightarrow IG \bot (ABC)\).

Trong \((SAG)\) kẻ SH||IG \( \Rightarrow SH \bot (ABC)\).

Dễ thấy khi đó $I G$ là đường trung bình của tam giác \(SAH \Rightarrow SH = 2IG\).

Tam giác $A B C$ đều cạnh \(2a \Rightarrow AG = \dfrac{2}{3} \cdot \dfrac{{2a\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{3}\).

Ta có \( \widehat {(SA,(ABC))} = \widehat {(SA,AH)} = \widehat {SAH} = {45^0 }\)

\( \Rightarrow \Delta AIG\) vuông cân tại \(G\).

Do đó \(IG = AG = \dfrac{{2a\sqrt 3 }}{3} \Rightarrow SH = 2IG = \dfrac{{4a\sqrt 3 }}{3}\).

Vậy thể tích khối chóp \(S \cdot ABC\) là

\(V = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3} \cdot \dfrac{{4a\sqrt 3 }}{3} \cdot \dfrac{{{{(2a)}^2}\sqrt 3 }}{4} = \dfrac{{4{a^3}}}{3}\)