Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\), với đáy \(ABCD\) là hình bình hành tâm \(O;AD,SA,AB\) đôi một vuông góc \(AD = 8,SA = 6\). \((P)\)là mặt phẳng qua trung điểm của \(AB\) và vuông góc với \(AB\). Thiết diện của \((P)\) và hình chóp có diện tích bằng?
Trả lời bởi giáo viên
Đáp án đúng: d
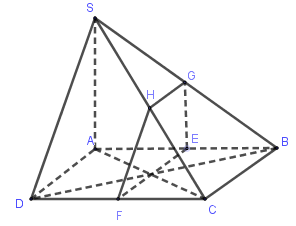
Gọi \(E\) là trung điểm của \(AB\).
Qua \(E\) kẻ \(EF \bot CD,EG \bot AB \Rightarrow \left( {EGF} \right) \bot AB\) và \(F,G\) là trung điểm của \(DC,SB\).
Do \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {EGF} \right) \cap \left( {ABCD} \right) = FE\\FE//BC\end{array} \right. \) \(\Rightarrow \left( {SBC} \right) \cap \left( {EGF} \right) = GH//BC\) (định lý giao tuyến ba mặt phẳng)
Suy ra \(H\) là trung điểm của \(SC\).
Vậy thiết diện là hình thang \(GHFE\).
Vì \(GE//SA\) nên \(GE \bot \left( {ABCD} \right) \Rightarrow GE \bot FE\) nên thiết diện là hình thang vuông.
\({S_{EGHF}} = \dfrac{{\left( {FE + GH} \right).GE}}{2} \) \(= \dfrac{{\left( {BC + \dfrac{1}{2}BC} \right).\dfrac{1}{2}SA}}{2} \) \( = \dfrac{{\left( {8 + 4} \right)3}}{2} = 18\)
Hướng dẫn giải:
- Xác định thiết diện, sử dụng tính chất đường thẳng vuông góc mặt phẳng: “Nếu một đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó”.
- Chứng thiết diện là hình thang vuông và tính diện tích.
