Câu hỏi:
3 năm trước
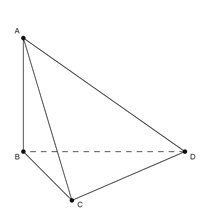
Cho tứ diện \(ABCD\) có cạnh $AB$, $BC$, $CD$ bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
Từ giả thiết ta có \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right. \Rightarrow AB \bot \left( {BCD} \right)\).
Do đó \(\left( {AC,\left( {BCD} \right)} \right) = \left( {AC,BC} \right) = \widehat {ACB}\).
Hướng dẫn giải:
- Tìm hình chiếu của \(A,C\) lên mặt phẳng \(\left( {BCD} \right)\) rồi suy ra góc cần tìm.
- Góc (không vuông) giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

