Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và \(AB \bot BC\). Dựng \(AH\) là đường cao của \(\Delta SAB\). Khẳng định nào sau đây sai?
Trả lời bởi giáo viên
Đáp án đúng: c
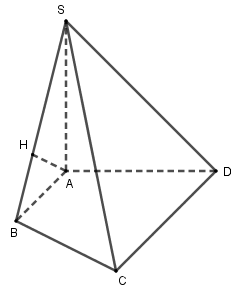
Do \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot CD\) hay A đúng.
Do \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\) \( \Rightarrow BC \bot AH\) nên B đúng.
Lại có \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\) nên D đúng.
Do \(AH \bot \left( {SBC} \right)\) nên nó không thể vuông góc với \(\left( {SCD} \right)\) nên C sai.

