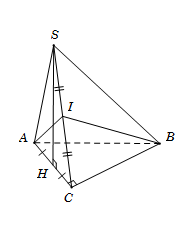
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $C$, mặt bên $SAC$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $I$ là trung điểm của $SC$. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
$\left( I \right):AI \bot SC$
$\left( {II} \right):\,\,\left( {SBC} \right) \bot \left( {SAC} \right)$
$\left( {III} \right):\,\,AI \bot BC$
$\left( {IV} \right):\,\,\left( {ABI} \right) \bot \left( {SBC} \right)$
Trả lời bởi giáo viên
Tam giác $SAC$ đều có $I$ là trung điểm của $SC$ nên $AI \bot SC$.
\( \Rightarrow \) Mệnh đề (I) đúng.
Gọi $H$ là trung điểm $AC$ suy ra $SH \bot AC$. Mà $\left( {SAC} \right) \bot \left( {ABC} \right)$ theo giao tuyến $AC$ nên $SH \bot \left( {ABC} \right)$ do đó $SH \bot BC$. Hơn nữa theo giả thiết tam giác $ABC$ vuông tại $C$ nên $BC \bot AC$.
Từ đó suy ra $BC \bot \left( {SAC} \right) \Rightarrow BC \bot AI.$ Do đó mệnh đề (III) đúng.
Từ mệnh đề (I) và (III) suy ra mệnh đề (IV) đúng.
Ta có : $\begin{array}{l}\left\{ \begin{array}{l}BC \bot AC\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right)\\BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAC} \right)\end{array}$
Vậy mệnh đề (II) đúng.