Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt đáy nằm trong hình vuông ABCD. Biết rằng SA và SC tạo với đáy các góc bằng nhau, góc giữa SB và đáy bằng 450, góc giữa SD và đáy bằng α với tanα=13. Tính thể tích khối chóp đã cho.
Trả lời bởi giáo viên
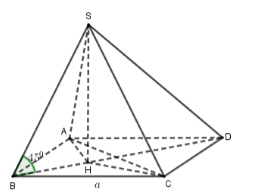
Gọi H là hình chiếu của S lên (ABCD).
Khi đó, ^SAH=^SCH vì hai góc này lần lượt là góc tạo bởi SA,SC với mặt phẳng đáy.
^SBH=450,tan^SDH=13.
Tam giác ΔSAH=ΔSCH⇒HA=HC ⇒H nằm trên trung trực của AC.
Mà BD là đường trung trực của AC nên H∈BD.
Lại có ^SBH=450⇒HB=HS,tan^SDH=13=SHHD ⇒HBHD=13⇒HBBD=14.
Mà BD=a√2⇒HB=a√24⇒SH=a√24
Vậy VS.ABCD=13SH.SABCD=13.a√24.a2=a3√212.
Hướng dẫn giải:
- Tìm vị trí điểm H trên mặt đáy, sử dụng các mối quan hệ góc bài cho.
- Tính SH và suy ra thể tích theo công thức V=13Bh với B là diện tích đáy, h là chiều cao.


