Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, các cạnh bên của hình chóp bằng nhau và bằng $2a$. Tính khoảng cách $d$ từ $A$ đến mặt phẳng $\left( SCD \right)$
Trả lời bởi giáo viên
Đáp án đúng: b
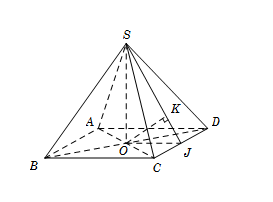
Gọi $O$ là tâm của đáy, suy ra $SO \bot \left( {ABCD} \right)$.
Ta có
\(\begin{array}{l}AO \cap \left( {SCD} \right) = C \Rightarrow \dfrac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \dfrac{{AC}}{{OC}} = 2\\ \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right).\end{array}\)
Gọi $J$ là trung điểm $CD$, suy ra $OJ \bot CD$.
Gọi $K$ là hình chiếu của $O$ trên $SJ$, suy ra $OK \bot SJ\,\,\,\left( 1 \right)$.
Ta có \(\left\{ \begin{array}{l}CD \bot OJ\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOJ} \right) \Rightarrow CD \bot OK\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow OK \bot \left( {SCD} \right) \Rightarrow d\left( {O;\left( {SCD} \right)} \right) = OK=\dfrac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }}\)
Ta có : \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {4{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{a\sqrt {14} }}{2} \Rightarrow OK = \dfrac{{\dfrac{{a\sqrt {14} }}{2}.\dfrac{a}{2}}}{{\sqrt {{{\left( {\dfrac{{a\sqrt {14} }}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} }} = \dfrac{{a\sqrt 7 }}{{\sqrt {30} }}\)
Vậy $d\left( {A;\left( {SCD} \right)} \right) = 2.OK = \dfrac{{2a\sqrt 7 }}{{\sqrt {30} }}.$
Hướng dẫn giải:
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng
