Câu hỏi:
3 năm trước
Cho hình chóp $S.ABC$ có \(SA \bot (ABC)\) và tam giác $ABC$ không vuông, gọi $H,{\rm{ }}K$ lần lượt là trực tâm các tam giác$ABC$ và $SBC$. Các đường thẳng $AH,{\rm{ }}SK,{\rm{ }}BC$ thỏa mãn:
Trả lời bởi giáo viên
Đáp án đúng: a
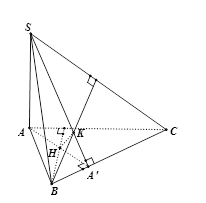
Gọi $AA'$ là đường cao của tam giác $ABC$ \( \Rightarrow AA' \bot BC\) mà
\(BC \bot SA\) nên \(BC \bot SA' \Rightarrow A' \in SK\) (vì \(K\) là trực tâm của tam giác)
Hướng dẫn giải:
Sử dụng tính chất \(\left\{ \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot b\)

