Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\),\(SA = BC = {\rm{ }}a,{\rm{ }}AC = 2a\). Khoảng cách từ điểm A đến mặt phẳng (SBC) là
Trả lời bởi giáo viên
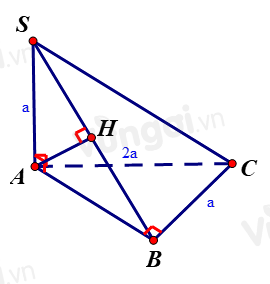
Bước 1: Kẻ AH vuông góc với SB. Chứng minh \(AH = d\left( {A,\left( {SBC} \right)} \right)\)
Kẻ AH vuông góc với SB.
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) = > SA \bot BC\\BC \bot AB\end{array} \right\}\\ \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\\AH \bot SB\\ \Rightarrow AH \bot \left( {SBC} \right)\end{array}\)
\( \Rightarrow AH = d\left( {A,\left( {SBC} \right)} \right)\)
Bước 2: Tính AH
Xét tam giác vuông ABC có: \(AB = \sqrt {A{C^2} - B{C^2}} = a\sqrt 3 \)
Xét tam giác vuông SAB có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}}\) \( = \dfrac{1}{{{a^2}}} + \dfrac{1}{{3{a^2}}} = \dfrac{4}{{3{a^2}}}\)
\( \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\)
Hướng dẫn giải:
Bước 1: Kẻ AH vuông góc với SB. Chứng minh \(AH \bot \left( {SBC} \right)\)
Bước 2: Tính AH