Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\)
Trả lời bởi giáo viên
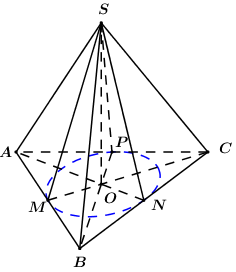
Gọi \(M,\,\,N,\,\,P\) lần lượt là hình chiếu của điểm \(S\) lên \(AB,\,\,BC,\,\,AC\) ta có:
\(\begin{array}{l}\,\,\,\,\,{S_{\Delta ABC}} = {S_{\Delta BCA}} = {S_{\Delta CAB}}\\ \Rightarrow \dfrac{1}{2}SM.AB = \dfrac{1}{2}SN.BC = \dfrac{1}{2}SP.CA\end{array}\)
Mà \(AB = BC = CA\,\,\left( {gt} \right) \Rightarrow SM = SN = SP\).
Gọi \(O\) là hình chiếu của \(S\) lên \(\left( {ABC} \right)\), ta có: \(\left\{ \begin{array}{l}AB \bot SM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OM\).
CMTT ta có \(ON \bot BC,\,\,OP \bot AC\).
Xét các tam giác vuông \(\Delta SOM,\,\,\Delta SON,\,\,\Delta SOP\) có:
\(\begin{array}{l}SO\,\,chung\\SM = SN = SP\,\,\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta SOM = \Delta SON = \Delta SOP\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow OM = ON = OP\), suy ra \(O\) cách đều các cạnh \(AB,\,\,BC,\,\,CA\) nên \(O\) là tâm đường tròn nội tiếp \(\Delta ABC\) hoặc \(O\) là tâm đường tròn bàng tiếp \(\Delta ABC\).
+ TH1: \(O\) là tâm đường tròn nội tiếp \(\Delta ABC\). Mà \(\Delta ABC\) đều nên \(O\) là đồng thời là trọng tâm tam giác đều \(ABC\). Khi đó ta có \(AN = \dfrac{{\sqrt 6 .\sqrt 3 }}{2} = \dfrac{{3\sqrt 2 }}{2},\,\,AO = \dfrac{2}{3}AN = \sqrt 2 \).
\( \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {18 - 2} = 4\).
\({S_{\Delta ABC}} = {\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 }}{2}\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}} = \dfrac{1}{3}.4.\dfrac{{3\sqrt 3 }}{2} = 2\sqrt 3 \).
TH2: \(O\) là tâm đường tròn bàng tiếp \(\Delta ABC\).
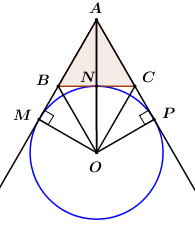
Gọi \(R\) là bán kính đường tròn bàng tiếp tam giác \(ABC\), \(p\) là nửa chu vi tam giác \(ABC\) \( \Rightarrow p = \dfrac{{3\sqrt 6 }}{2}\).
Khi đó ta có \({S_{ABC}} = \left( {p - BC} \right).R\) \( \Rightarrow {\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = \left( {\dfrac{{3\sqrt 6 }}{2} - \sqrt 6 } \right).R \Leftrightarrow R = \dfrac{{3\sqrt 2 }}{2}\).
Có \(AN = \dfrac{{\sqrt 6 .\sqrt 3 }}{2} = \dfrac{{3\sqrt 2 }}{2}\) \( \Rightarrow OA = AN + ON = 3\sqrt 2 \).
\( \Rightarrow SA > OA = 3\sqrt 2 \) (quan hệ giữa đường vuông góc và đường xiên)
\( \Rightarrow SB = 3\sqrt 2 \).
Áp dụng định lí Pytago trong tam giác vuông \(OBM\) có: \(OB = \sqrt {O{M^2} + B{M^2}} = \sqrt {{{\left( {\dfrac{{3\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{\sqrt 6 }}{2}} \right)}^2}} = \sqrt 6 \).
Áp dụng định lí Pytago trong tam giác vuông \(SOB\) có: \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {{{\left( {3\sqrt 2 } \right)}^2} - {{\left( {\sqrt 6 } \right)}^2}} = 2\sqrt 3 \).
Khi đó ta có \({V_{S.ABC}} = \dfrac{1}{3}.SO.{S_{ABC}} = \dfrac{1}{3}.2\sqrt 3 .{\left( {\sqrt 6 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = 3\).
Vậy \(\min {V_{S.ABC}} = 3\).

