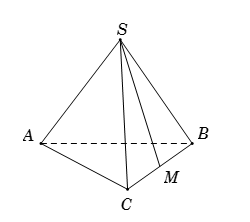
Cho hình chóp \(S.ABC\) có \(AB = AC\) và \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng chéo nhau \(SA\) và \(BC.\)
Trả lời bởi giáo viên
Xét \(\overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .\left( {\overrightarrow {SC} - \overrightarrow {SB} } \right) = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} \)
$ = \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.\cos \left( {\overrightarrow {SA} ,\overrightarrow {SC} } \right) - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|.\cos \widehat {SAB}$
$ = SA.SC.\cos \widehat {ASC} - SA.SB.\cos \widehat {ASB}.$ \(\left( 1 \right)\)
Ta có \(\left\{ \begin{array}{l}SA{\rm{ chung}}\\AB = AC\\\widehat {SAB} = \widehat {SAC}\end{array} \right. \Rightarrow \Delta SAB = \Delta SAC{\rm{ }}\left( {c - g - c} \right)\).
Suy ra \(\left\{ \begin{array}{l}SC = SB\\\widehat {ASC} = \widehat {ASB}\end{array} \right.\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(\overrightarrow {SA} .\overrightarrow {BC} = 0\). Vậy \(SA \bot BC\).
Hướng dẫn giải:
Tính tích vô hướng \(\overrightarrow {SA} .\overrightarrow {BC} \) rồi suy ra đáp án.

