Cho hình bình hành \(ABCD\) có \(A\left( { - 2;3} \right)\) và tâm \(I\left( {1;1} \right)\). Biết điểm \(K\left( { - 1;2} \right)\) nằm trên đường thẳng $AB$ và điểm $D$ có hoành độ gấp đôi tung độ. Chọn kết luận đúng:
Trả lời bởi giáo viên
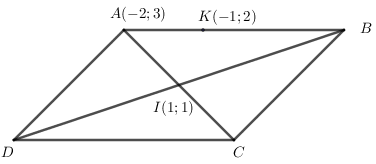
Gọi \(D\left( {2a;a} \right) \Rightarrow B\left( {2 - 2a;2 - a} \right)\)
\(\overrightarrow {AK} \left( {1; - 1} \right),\,\,\overrightarrow {AB} \left( {4 - 2a; - 1 - a} \right)\)
Vì \(\overrightarrow {AK} ,\,\,\overrightarrow {AB} \) cùng phương nên \(\dfrac{{4 - 2a}}{1} = \dfrac{{ - 1 - a}}{{ - 1}} \Rightarrow a = 1 \) \(\Rightarrow D\left( {2;1} \right),\,\,B\left( {0;1} \right)\)
Hướng dẫn giải:
- Gọi tọa độ điểm \(D\left( {2a;a} \right)\), tìm tọa độ \(B\) theo \(a\)
- Tìm \(a\) với chú ý \(\overrightarrow {AK} \) và \(\overrightarrow {AB} \) cùng phương:
Điều kiện để hai véc tơ \(\overrightarrow u ,\overrightarrow v \) cùng phương là \(\dfrac{{{u_1}}}{{{v_1}}} = \dfrac{{{u_2}}}{{{v_2}}}\) với \({v_1}.{v_2} \ne 0\)

