Câu hỏi:
3 năm trước
Cho hàm số $y = {x^4} - 2{x^2} + 2$. Diện tích $S$ của tam giác có $3$ đỉnh là $3$ điểm cực trị của đồ thị hàm số đã cho có giá trị là
Trả lời bởi giáo viên
Đáp án đúng: c
$\begin{array}{*{20}{l}}{y = {x^4} - 2{x^2} + 2{\mkern 1mu} {\mkern 1mu} (C) \Rightarrow y' = 4{x^3} - 4x}\\{y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm 1}\end{array}} \right.}\end{array}$
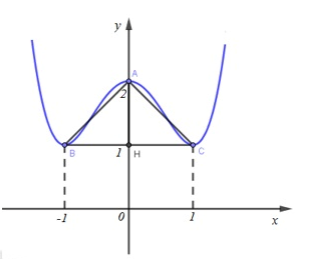
Tọa độ các điểm cực trị của $\left( C \right)$ là: $A(0;2),{\mkern 1mu} {\mkern 1mu} B( - 1;1),{\mkern 1mu} C(1;1)$.
Diện tích tam giác $ABC:$ ${S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.(2 - 1).(1 - ( - 1)) = 1$
Hướng dẫn giải:
- Tìm các điểm cực trị của đồ thị hàm số.
- Tính diện tích tam giác theo công thức $S = \frac{1}{2}ah$

