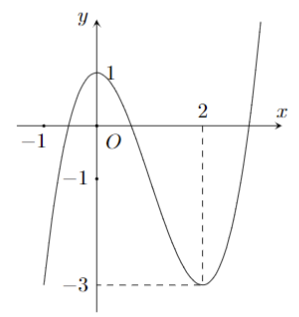
Cho hàm số \(y = f(x)\) như hình vẽ. Số nghiệm của phương trình \(\left| {f\left( {{x^3} - 3{x^2} + 2} \right)} \right| - 1 = 0\) là

Ta có \(\left| {f\left( {{x^3} - 3{x^2} + 2} \right)} \right| - 1 = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( {{x^3} - 3{x^2} + 2} \right) = 1}\\{f\left( {{x^3} - 3{x^2} + 2} \right) =  - 1}\end{array}} \right.\)

Từ đồ thị hàm số \(y = f(x)\), ta có

+) \(f\left( {{x^3} - 3{x^2} + 1} \right) = 1 \Leftrightarrow {x^3} - 3{x^2} + 2 = 0\) hoặc \({x^3} - 3{x^2} + 2 = {x_0}\left( {2 < {x_0}} \right)\).

+) \(f\left( {{x^3} - 3{x^2} + 1} \right) =  - 1 \Leftrightarrow {x^3} - 3{x^2} + 2 = {x_1}\) hoặc \({x^3} - 3{x^2} + 2 = {x_2}\) hoặc \({x^3} - 3{x^2} + 2 = {x_3}\), trong đó \(\left( { - 1 < {x_1} < 0,0 < {x_2} < 2,2 < {x_3}} \right)\).

Xét hàm số \(y = g(x) = {x^3} - 3{x^2} + 2\), xác định và liên tục trên \(\mathbb{R}\).

Ta có \({g^\prime }(x) = 3{x^2} - 6x = 3x(x - 2),\) \({g^\prime }(x) = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).

Bảng biến thiên của \(g(x)\) như hình sau.

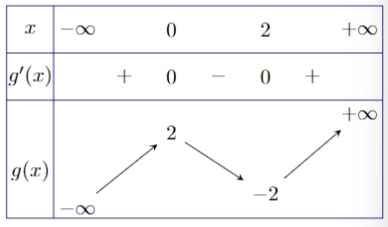
Từ bảng biến thiên của hàm số \(y = g(x) = {x^3} - 3{x^2} + 2\), ta có

- Phương trình \({x^3} - 3{x^2} + 2 = 0\) có 3 nghiệm phân biệt.

- Phương trình \({x^3} - 3{x^2} + 2 = {x_0}\left( {{x_0} > 2} \right)\) có 1 nghiệm.

- Phương trình \({x^3} - 3{x^2} + 2 = {x_1}\left( { - 1 < {x_1} < 0} \right)\) có 3 nghiệm phân biệt.

- Phương trình \({x^3} - 3{x^2} + 2 = {x_2}\left( {0 < {x_2} < 2} \right)\) có 3 nghiệm phân biệt.

- Phương trình \({x^3} - 3{x^2} + 2 = {x_3}\left( {2 < {x_3}} \right)\) có 1 nghiệm phân biệt.

Vậy phương trình \(\left| {f\left( {{x^3} - 3{x^2} + 2} \right)} \right| - 1 = 0\) có 11 nghiệm phân biệt.