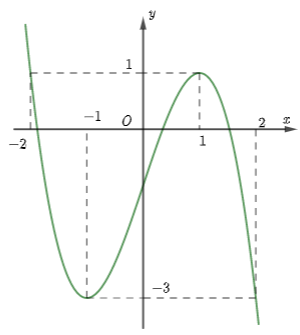
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ:

Số nghiệm thực của phương trình \(f\left( {2 - f\left( x \right)} \right) = 1\) là

Giới hạn nào sau đây bằng 0?

Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_5} = 9\), công bội \(q = \dfrac{1}{3}\). Tìm \({u_2}\).

Chọn ngẫu nhiên lần lượt hai số nguyên dương bé hơn 100. Tính xác suất để hiệu hai số vừa được chọn là một số lẻ.

Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình chữ nhật. Biết \(AD = 2a\), \(SA = a\). Khoảng cách từ \(A\) đến \(\left( {SCD} \right)\) bằng

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(SA\) vuông góc với mặt phẳng đáy. Tính cosin góc giữa hai đường thẳng \(SD\) và \(BC\), biết \(AD = DC = a\), \(AB = 2a\), \(SA = \dfrac{{2a\sqrt 3 }}{3}\).

Điểm nào dưới đây thuộc đồ thị của hàm số \(y = {x^4} + {x^2} - 2\) ?

Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là