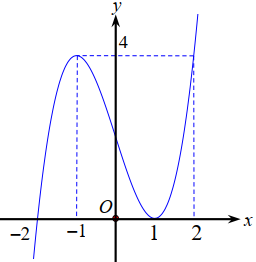
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Số các giá trị nguyên của \(m\) để phương trình \(f\left( {2\sin x} \right) = m + 3m\) có đúng ba nghiệm phân biệt thuộc đoạn \(\left[ { - \pi ;\,\pi } \right]\) là
Trả lời bởi giáo viên
Bước 1: Sử dụng phương pháp ghép trục
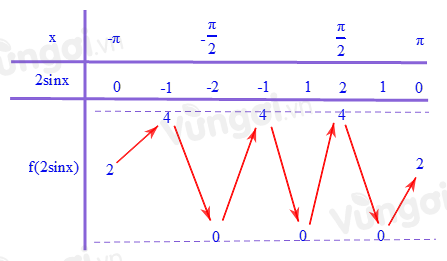
Bước 2: Biện luận m
Từ bảng trên ta thấy để phương trình \(f\left( {2\sin x} \right) = m + 3m\) có đúng ba nghiệm phân biệt thuộc đoạn \(\left[ { - \pi ;\,\pi } \right]\) thì \(y = {m^2} + 3m\)
Khi đó \(\left[ \begin{array}{l}{m^2} + 3m = 0\\{m^2} + 3m = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0;m = - 3\\m = 1;m = - 4\end{array} \right.\)
Vậy 4 giá trị của m thỏa mãn.
Hướng dẫn giải:
Bước 1: Sử dụng phương pháp ghép trục
Bước 2: Biện luận m