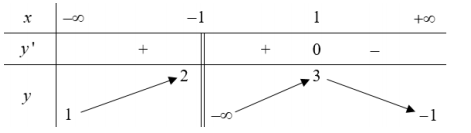
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau
Khẳng định nào sau đây sai?
Trả lời bởi giáo viên
Từ BBT ta thấy hàm số đồng biến trên \(\left( { - \infty ; - 1} \right);\left( { - 1;1} \right)\) nên B sai vì trên khoảng \(\left( { - \infty ;1} \right)\) thì hàm số gián đoạn tại \(x = - 1.\)
Hàm số nghịch biến trên \(\left( {1; + \infty } \right)\) nên C đúng. Dễ thấy A đúng.
Lại có \(\mathop {\lim }\limits_{x \to - {1^ + }} x = - \infty \) nên \(x = - 1\) là TCĐ của đồ thị hàm số
Và \(\mathop {\lim }\limits_{x \to - \infty } y = 1;\,\mathop {\lim }\limits_{x \to + \infty } y = - 1\) nên \(y = 1;y = - 1\) là hai tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có ba tiệm cận nên D đúng.
Hướng dẫn giải:
Sử dụng cách đọc bảng biến thiên
Hàm số \(y = f\left( x \right)\) có \(y' > 0\) trên \(\left( {a;b} \right)\) thì đồng biến trên \(\left( {a;b} \right)\)
Sử dụng định nghĩa tiệm cận
Đồ thị hàm số \(y = f\left( x \right)\) nhận đường thẳng \(y = {y_0}\) làm tiệm cận ngang nếu thỏa mãn 1 trong các điều kiện sau \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0};\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\)
Đồ thị hàm số \(y = f\left( x \right)\) nhận đường thẳng \(x = {x_0}\) làm tiệm cận đứng nếu thỏa mãn 1 trong các điều kiện sau \(\mathop {\lim }\limits_{x \to x_0^ + } x = + \infty ;\mathop {\lim }\limits_{x \to x_0^ + } x = - \infty ;\mathop {\lim }\limits_{x \to x_0^ - } x = + \infty ;\mathop {\lim }\limits_{x \to x_0^ - } x = - \infty \)


