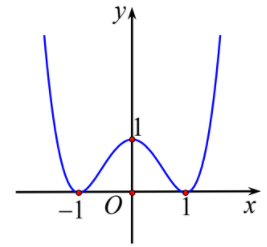
Cho hàm số $y = {\rm{ }}f\left( x \right).$Biết hàm số $y = {\rm{ }}f'\left( x \right)$ là hàm số bậc 4 trùng phương có đồ thị như hình vẽ.

Số điểm cực trị của hàm số $y = f\left( {{e^{{x^2} + 3x + 5}}} \right) - 2{e^{{x^2} + 3x + 5}}$ là

Từ các chữ số 1,2,3,4,5,6,7,8,9 lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó chia hết cho 3

Cho S là tập nghiệm của bất phương trình ${\log _5}\left( {{x^2} + 2x + 3} \right) > {\log _5}\left( {{x^2} + 4x + 2 + m} \right) - 1$. Số giá trị nguyên của tham số m để $\left( {1;2} \right) \subset S$ là

Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho 4 điểm A(1;5;4), B(-3;1;4),  C(5;4;1), D(-2;1;-3). Bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng

Gọi ${V_1},{V_2}$ lần lượt là thể tích của khối tứ diện đều và khối lập phương có chung mặt cầu ngoại tiếp. Khi đó, $\dfrac{{{V_1}}}{{{V_2}}}$ bằng

Xét các số phức z thỏa mãn $\left| {z - i} \right| = \left| {z + 3i} \right|$. Giá trị nhỏ nhất của biểu thức$\left| {z + 2 - i} \right| + \left| {z - 3 - 3i} \right|$ bằng

Một lô hàng có 30 sản phẩm trong đó có 5 phế phẩm. Lấy ngẫu nhiên đồng thời 6 sản phẩm của lô hàng đó. Xác suất để trong 6 sản phẩm lấy ra có không quá 2 phế phẩm là

Cho một tấm tôn hình vuông có cạnh bằng a. Người ta cắt 4 góc của tấm tôn để được một tấm tôn mới như hình vẽ.

Từ tấm tôn mới, người ta gặp được một hình chóp tứ giác đều. Để khối chóp thu được có thể tích lớn nhất thì diện tích các miếng tôn bỏ đi là