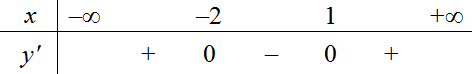Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ.

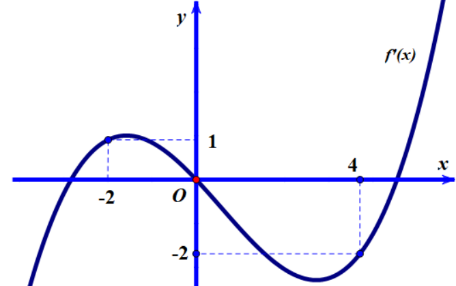
Hàm số \(g\left( x \right) = 4f\left( {{x^2} - 4} \right) + {x^4} - 8{x^2}\) có bao nhiêu điểm cực tiểu?

\(g'\left( x \right) = 8xf'\left( {{x^2} - 4} \right) + 4{x^3} - 16x\)\( = 4x\left[ {2f'\left( {{x^2} - 4} \right) + {x^2} - 4} \right]\)

\(g'\left( x \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 4} \right) =  - \dfrac{1}{2}\left( {{x^2} - 4} \right)\left( 1 \right)\end{array} \right.\)

Đặt \(t = {x^2} - 4\), khi đó (1) trở thành :

\(f'\left( t \right) =  - \dfrac{1}{2}t\)\( \Leftrightarrow \left[ \begin{array}{l}t =  - 2\\t = 0\\t = 4\end{array} \right.\)

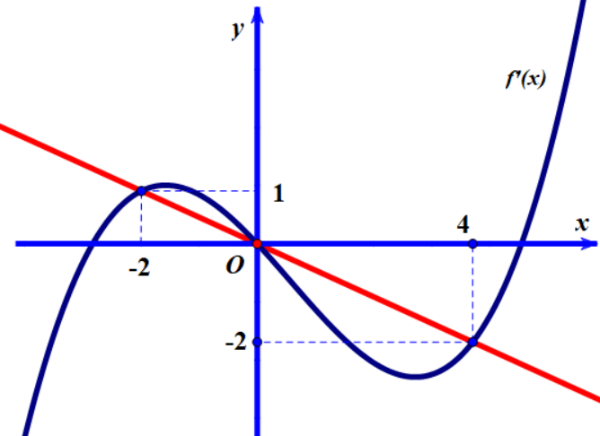
Với \(\left[ \begin{array}{l}t =  - 2\\t = 0\\t = 4\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}{x^2} - 4 =  - 2\\{x^2} - 4 = 0\\{x^2} - 4 = 4\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x =  \pm \sqrt 2 \\x =  \pm 2\\x =  \pm 2\sqrt 2 \end{array} \right.\).

Do \(f\left( x \right)\) là hàm số bậc bốn nên \(f'\left( x \right)\) là hàm số bậc ba; đồng thời ta có \(\mathop {\lim }\limits_{x \to  - \infty } f'\left( x \right) =  - \infty \), \(\mathop {\lim }\limits_{x \to  + \infty } f'\left( x \right) =  + \infty \)\( \Rightarrow \mathop {\lim }\limits_{x \to  \pm \infty } f\left( x \right) =  + \infty \)

Bảng biến thiên:

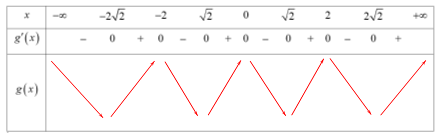
Vậy hàm số \(g\left( x \right) = 4f\left( {{x^2} - 4} \right) + {x^4} - 8{x^2}\) có bốn điểm cực tiểu.