Cho hàm số bậc ba \(y = f(x)\) có đồ thị như hình vẽ bên.

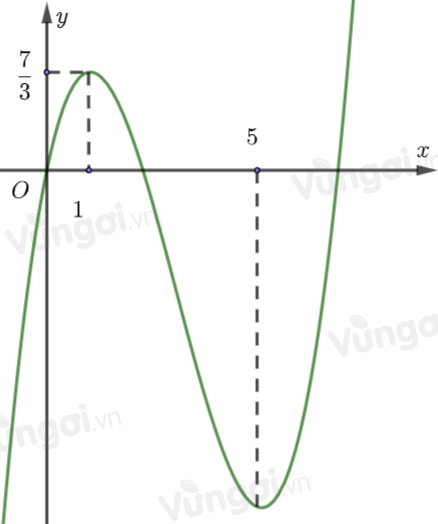
Có tất cả bao nhiêu số nguyên \(m\) thuộc đoạn \([ - 10;10]\) để hàm số \(y = {e^{f(x) - m{x^2} + (m + 4)x}}\) đồng biến trên khoảng \((1; + \infty )\)

Gọi hàm số \(y = f(x)\) là \(y = a{x^3} + b{x^2} + cx + d\)

Khi đó, \(y\left( 0 \right) = 0;y\left( 1 \right) = \dfrac{7}{3}y'\left( 1 \right) = 0;y'\left( 5 \right) = 0\)

Ta có hệ phương trình sau: \(\left\{ \begin{array}{l}d = 0\\a + b + c + d = \dfrac{7}{3}\\3a + 2b + c = 0\\75a + 10b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{3}\\b =  - 3\\c = 5\\d = 0\end{array} \right.\)

\( \Rightarrow y = \dfrac{1}{3}{x^3} - 3{x^2} + 5x\)

Ta có: \(y' = \left[ {f'\left( x \right) - 2mx + m + 4} \right]{e^{f(x) - m{x^2} + (m + 4)x}}\)

\(\begin{array}{l} = \left( {{x^2} - 6x + 5 - 2mx + m + 4} \right){e^{f(x) - m{x^2} + (m + 4)x}}\\ = \left( {{x^2} - 6x + 9 - 2mx + m} \right){e^{f(x) - m{x^2} + (m + 4)x}}\\y' \ge 0\forall x \in \left( {1; + \infty } \right)\\ \Leftrightarrow {x^2} - 6x + 9 - 2mx + m \ge 0\forall x \in \left( {1; + \infty } \right)\\ \Leftrightarrow 2mx - m \le {x^2} - 6x + 9\forall x \in \left( {1; + \infty } \right)\\ \Leftrightarrow m\left( {2x - 1} \right) \le {\left( {x - 3} \right)^2}\forall x \in \left( {1; + \infty } \right)\\ \Leftrightarrow m \le \dfrac{{{{\left( {x - 3} \right)}^2}}}{{2x - 1}}\forall x \in \left( {1; + \infty } \right)\end{array}\)

Xét hàm số \(y = \dfrac{{{{\left( {x - 3} \right)}^2}}}{{2x - 1}}\) trên \((1; + \infty )\)

Ta có:

\(\begin{array}{l}y' = \dfrac{{2\left( {x - 3} \right)\left( {2x - 1} \right) - 2{{\left( {x - 3} \right)}^2}}}{{{{\left( {2x - 1} \right)}^2}}}\\ = \dfrac{{2\left( {x - 3} \right)\left( {x + 2} \right)}}{{{{\left( {2x - 1} \right)}^2}}}\\y' = 0 \Leftrightarrow x = 3\end{array}\)

Lập bảng biến thiên:

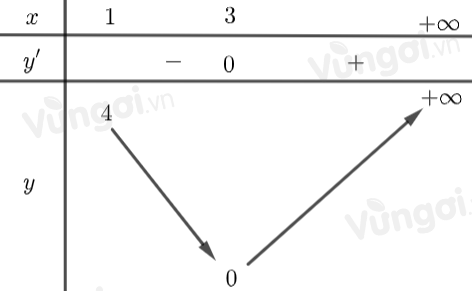
=> \(\min y = 0\)

Khi đó

\(\begin{array}{l}m \le \dfrac{{{{\left( {x - 3} \right)}^2}}}{{2x - 1}}\forall x \in \left( {1; + \infty } \right) \Leftrightarrow m \le \min y = 0\\ \Rightarrow  - 10 \le m \le 0\end{array}\)