Cho hai hàm số bậc bốn \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có các đồ thị như hình dưới đây (2 đồ thị có đúng 3 điểm chung).
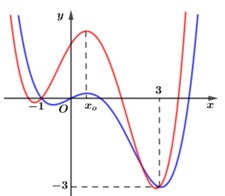
Số điểm cực trị của hàm số \(h\left( x \right) = {f^2}\left( x \right) + {g^2}\left( x \right) - 2f\left( x \right).g\left( x \right)\) là:
Trả lời bởi giáo viên
Ta có:
\(h\left( x \right) = {\left[ {f\left( x \right) - g\left( x \right)} \right]^2}\)
\( \Rightarrow h'\left( x \right) = 2\left[ {f\left( x \right) - g\left( x \right)} \right].\left[ {f\left( x \right) - g\left( x \right)} \right]'\) \( = 2\left[ {f\left( x \right) - g\left( x \right)} \right]\left[ {f'\left( x \right) - g'\left( x \right)} \right].\)
Cho \(h'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) - g\left( x \right) = 0\,\,\,\,\,\,\left( 1 \right)\\f'\left( x \right) - g'\left( x \right) = 0\,\,\,\left( 2 \right)\end{array} \right.\)
Từ đồ thị hàm số ta thấy phương trình (1) có 3 nghiệm phân biệt \(\left[ \begin{array}{l}x = - 1\\x = {x_1} \in \left( { - 1;3} \right)\\x = 3\end{array} \right.\) và đa thức \(f\left( x \right) - g\left( x \right)\) đổi dấu khi qua các nghiệm này. Do đó các nghiệm trên là các nghiệm bội lẻ của (1). Mà \(f\left( x \right)\) và \(g\left( x \right)\) đều là các đa thức bậc 4 nên bậc của phương trình (1) nhỏ hơn hoặc bằng 4. Từ đó suy ra phương trình (1) là phương trình bậc 3.
Do đó phương trình (1) là phương trình bậc 3 có 3 nghiệm phân biệt nên phương trình (2) có 2 nghiệm phân biệt không trùng với các nghiệm của phương trình (1).
Suy ra phương trình \(h'\left( x \right) = 0\) có 5 nghiệm phân biệt và \(h'\left( x \right)\) đổi dấu qua các nghiệm này nên hàm số \(h\left( x \right)\) có 5 điểm cực trị.
Hướng dẫn giải:
- Tính đạo hàm hàm số \(g\left( x \right)\).
- Sử dụng tương giao, đặt ẩn phụ và giải phương trình \(g'\left( x \right) = 0\).
- Xác định số nghiệm bội lẻ của phương trình \(g'\left( x \right) = 0\), từ đó suy ra số điểm cực trị của hàm số \(g\left( x \right)\) chính là số nghiệm bội lẻ của phương trình \(g'\left( x \right) = 0\).

