Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ các đường kính $AOB;AO'C$. Gọi $DE$ là tiếp tuyến chung của hai đường  tròn  $\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)$. Gọi $M$ là giao điểm của $BD$ và $CE$. Tính diện tích tứ giác $ADME$ biết $\widehat {DOA} = 60^\circ $ và $OA = 6\,cm.$

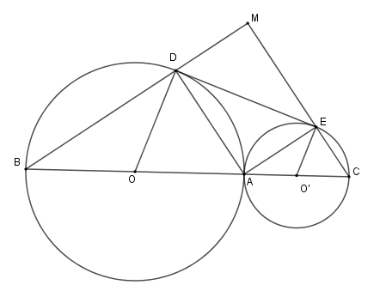
Chứng minh tương tự câu trước ta có được $\widehat {DAE} = 90^\circ $

Mà \(\widehat {BDA} = 90^\circ \) ( vì tam giác \(BAD\) có cạnh \(AB\) là đường kính của \(\left( O \right)\) và \(D \in \left( O \right)\) ) nên \(BD \bot AD \Rightarrow \widehat {MDA} = 90^\circ .\) Tương tự ta có \(\widehat {MEA} = 90^\circ .\)

Nên tứ giác $DMEA$ là hình chữ nhật.

Xét tam giác $OAD$ cân tại $O$ có $\widehat {DOA} = 60^\circ $ nên $\Delta DOA$ đều,

suy ra $OA = AD = 6\,cm$ và $\widehat {ODA} = 60^\circ $

$ \Rightarrow \widehat {ADE} = 30^\circ $.

Xét tam giác $ADE$ ta có

$EA = AD.\tan \widehat {EDA} = 6.\tan 30^\circ  = 2\sqrt 3 $

${S_{DMEA}} = AD.AE = 6.2\sqrt 3  = 12\sqrt 3 \,\,c{m^2}$.