Câu hỏi:
2 năm trước
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $MN$ với $M \in \left( O \right)$; $N \in \left( {O'} \right)$. Gọi $P$ là điểm đối xứng với $M$ qua $OO'$; $Q$ là điểm đối xứng với $N$ qua $OO'$.
Khi đó, tứ giác $MNQP$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: a
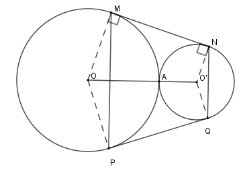
Vì $P$ là điểm đối xứng với $M$ qua $OO'$;
$Q$ là điểm đối xứng với $N$ qua $OO'$ nên $MN = PQ$;
$P \in \left( O \right);Q \in \left( {O'} \right)$
và $MP \bot OO';NQ \bot OO' $
$\Rightarrow MP{\rm{//}}NQ$ mà $MN = PQ$
nên $MNPQ$ là hình thang cân.
Hướng dẫn giải:
Sử dụng tính chất tiếp tuyến và dấu hiệu nhận biết các hình đặc biệt
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
