Câu hỏi:
2 năm trước
Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .
Trả lời bởi giáo viên
Đáp án đúng: a
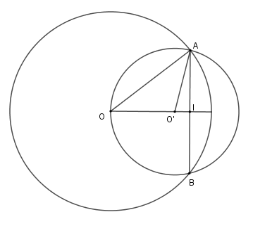
Ta có: $AI = \dfrac{1}{2}AB = 12\,\ cm$
Theo định lý Pytago ta có
$O{I^2} = O{A^2}-A{I^2} = 256$ $ \Rightarrow $ $OI = 16 \,\ cm$ và $O'I = \sqrt {O'{A^2} - I{A^2}} = 9 \,\ cm$
Do đó: $OO' = OI-O'I = 16-9 = 7\left( {cm} \right)$ .
Hướng dẫn giải:
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và định lý Pytago
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
