Câu hỏi:
2 năm trước
Cho hai đường thẳng \(a\) và \(b\) song song với nhau, cách nhau một khoảng là \(6\,cm\). Một đường tròn \(\left( O \right)\) tiếp xúc với \(a\) và \(b\). Hỏi tâm \(O\) di động trên đường nào?
Trả lời bởi giáo viên
Đáp án đúng: d
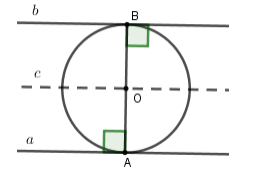
Kẻ đường thẳng \(OA \bot a\) tại \(A\) cắt \(b\) tại \(B\) thì \(OB \bot b\) tại \(B\) vì \(a{\rm{//}}b\).
Vì \(\left( O \right)\) tiếp xúc với cả \(a,b\) nên \(OA = OB\). Lại có \(AB = 6\,cm \Rightarrow OA = OB = \dfrac{6}{2} = 3\,cm\)
Hay tâm \(O\) cách \(a\) và \(b\) một khoảng cùng bằng \(3\,cm\)
Nên \(O\) chạy trên đường thẳng \(c\) song song và cách đều \(a,b\) một khoảng \(3\,cm.\)
Hướng dẫn giải:
Xác định xem tâm đường tròn cách đường thẳng cho trước một khoảng bằng bao nhiêu rồi sử dụng tính chất điểm cách đều đường thẳng để xác định quỹ tích.


