Câu hỏi:
2 năm trước
Cho hai điểm $A,B$ nằm trên cùng một nửa mặt phẳng bờ là đường thẳng $d$ . Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. Tìm trên đường thẳng $d$ điểm $M$ sao cho tổng $MA + MB$ nhỏ nhất. Chọn khẳng định đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: b
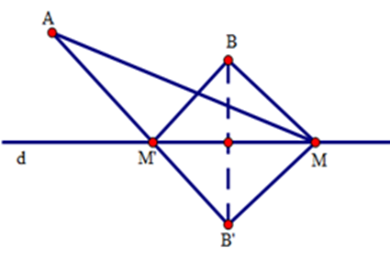
Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. $B'$ cố định.
Ta có $MB = MB'$ (tính chất đối xứng trục).
Xét ba điểm $M,{\rm{ }}A,{\rm{ }}B'$ ta có $MA + MB' \ge AB'$
Do đó $MA + MB \ge AB'$
Dấu “=” xảy ra khi và chỉ khi $A,M,B'$ thẳng hàng theo thứ tự đó hay $M$ là giao điểm của đoạn $AB'$ và đường thẳng $d$ .
Vậy khi \(M \equiv M'\) là giao điểm của đoạn thẳng $AB'$ và đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất, trong đó $B'$ là điểm đối xứng của $B$ qua $d$ .
Hướng dẫn giải:
Ta nhân thấy nếu $A,{\rm{ }}B$ nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất là đoạn $AB$ . Do vậy ta tìm cách đưa bài toán về trường hợp này.
Bằng cách dựng $B'$ đối xứng với $B$ qua $d$ ta đưa bài toán đã cho về trường hợp nêu trên vì $MB = MB'$ .
