Câu hỏi:
2 năm trước
Cho đường tròn \(\left( O \right)\) , đường kính \(AB\) . Lấy điểm \(C\) là trung điểm đoạn \(OB.\) Kẻ dây \(MN\) qua \(C\) và dây \(AD//MN\). So sánh độ dài \(AD\) và \(MN\) .
Trả lời bởi giáo viên
Đáp án đúng: d
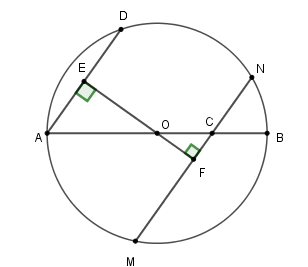
Kẻ đường thẳng qua \(O\) vuông góc với \(AD\) tại \(E\) và cắt \(MN\) tại \(F\) thì \(EF \bot MN\) tại \(F\) vì \(AC{\rm{//MN}}\) .
Xét hai tam giác vuông \(OEA\) và tam giác \(OFC\) có \(\widehat {AEO} = \widehat {OFC} = 90^\circ ;\widehat {AOE} = \widehat {FOC}\) (đối đỉnh)
Nên \(\Delta AEO \backsim \Delta CFO\,\left( {g - g} \right)\)\( \Rightarrow \dfrac{{OE}}{{OF}} = \dfrac{{OA}}{{OC}}\) mà \(OA = OB = 2.OC \Rightarrow \dfrac{{OE}}{{OF}} = \dfrac{{OA}}{{OC}} = 2 \Rightarrow OE = 2OF\)
Hay \(OE > OF\) suy ra \(AD < MN\) (dây nào xa tâm hơn thì dây đó nhỏ hơn).
Hướng dẫn giải:
Sử dụng mối liên hệ giữa dây và khoảng cách từ tâm đến dây.
“Trong một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn”
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
