Câu hỏi:
2 năm trước
Cho đường tròn \(\left( O \right),\) dây cung \(AB\) và \(CD\) với \(CD = AB\). Giao điểm \(K\) của các đường thẳng \(AB\) và \(CD\) nằm ngoài đường tròn. Vẽ đường tròn \(\left( {O;OK} \right),\) đường tròn này cắt \(KA\) và \(KC\) lần lượt tại \(M\) và \(N\) . So sánh KM và KN.
Trả lời bởi giáo viên
Đáp án đúng: c
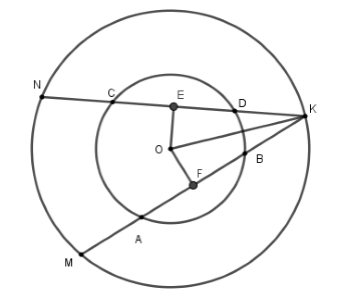
Xét đường tròn \(\left( {O;OB} \right)\)
Kẻ \(OE \bot CD;OF \bot AB\) tại \(E,F\) mà \(CD = AB \Rightarrow OE = OF\) (hai dây bằng nhau thì cách đều tâm)
Xét đường tròn \(\left( {O;OK} \right)\) có \(OE \bot KN;OF \bot KM\) tại \(E,F\) mà \(OE = OF \Rightarrow KN = KM\)( liên hệ giữa dây và khoảng cách từ tâm đến dây)

