Cho đường tròn \(\left( {O;8\,cm} \right).\) Dây \(AB\) và \(CD\) song song, có độ dài lần lượt là \(14cm\) và \(10\,cm\) .Tính khoảng cách giữa hai dây.
Trả lời bởi giáo viên
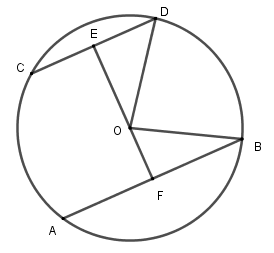
Kẻ đường thẳng qua \(O\) vuông góc với \(CD\) tại \(E\) và cắt \(AB\) tại \(F\) thì \(EF \bot AB\) vì \(AB\,{\rm{//}}\,CD\).
Khi đó \(E\) là trung điểm của \(CD\) và \(F\) là trung điểm của \(AB\) ( đường kính vuông góc với dây thì đi qua trung điểm dây đó). Nên \(ED = \dfrac{{CD}}{2} = 5cm;\,FB = \dfrac{{AB}}{2} = 7\,cm\); \(OD = OB = 8\,cm\)
Áp dụng định lý Pytago cho tam giác vuông \(OED\) ta được \(OE = \sqrt {O{D^2} - E{D^2}} = \sqrt {{8^2} - {5^2}} = \sqrt {39} \,cm\)
Áp dụng định lý Pytago cho tam giác vuông \(OFB\) ta được \(OF = \sqrt {O{B^2} - F{B^2}} = \sqrt {{8^2} - {7^2}} = \sqrt {15} \,cm\)
Vậy khoảng cách giữa hai dây là \(EF = OE + OF = \sqrt {39} + \sqrt {15} \,cm\).
Hướng dẫn giải:
Sử dụng liên hệ giữa dây và đường kính: “Đường kính vuông góc với dây thì đi qua trung điểm của dây đó” để áp dụng định lý Pytago cho tam giác vuông phù hợp.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
