Câu hỏi:
2 năm trước
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
Trả lời bởi giáo viên
Đáp án đúng: a
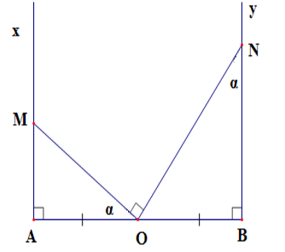
Theo đề bài ta có: \(AB = 2a \Rightarrow OA = OB = a\)
Ta có: \(\widehat {ONB} = \widehat {AOM} = \alpha \) (cùng phụ với \(\widehat {BON}\) )
Xét \(\Delta AOM\) có \(\widehat A = 90^\circ \)
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OA = OM.\cos \alpha \Rightarrow OM = \dfrac{a}{{\cos \alpha }}\)
Xét \(\Delta BON\) có \(\widehat B = 90^\circ \)
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OB = ON.\sin \alpha \Rightarrow ON = \dfrac{a}{{\sin \alpha }}\)
Vậy diện tích tam giác \(MON\) là: \(\dfrac{1}{2}OM.ON = \dfrac{1}{2}.\dfrac{a}{{\cos \alpha }}.\dfrac{a}{{\sin \alpha }} = \dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
Hướng dẫn giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông
Áp dụng công thức tính diện tích tam giác vuông
