Câu hỏi:
2 năm trước
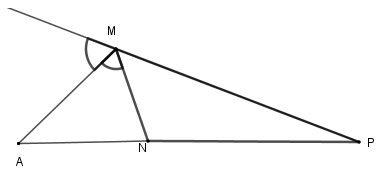
Cho \(\Delta MNP,MA\) là phân giác ngoài của góc \(M\), biết \(\dfrac{{NA}}{{PA}} = \dfrac{1}{3}\). Hãy chọn khẳng định sai:
Trả lời bởi giáo viên
Đáp án đúng: c
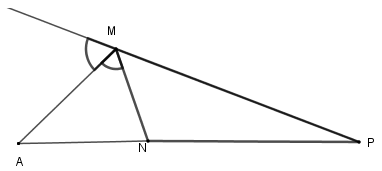
Theo tính chất đường phân giác ngoài của tam giác ta có: \(\dfrac{{MN}}{{MP}} = \dfrac{{NA}}{{PA}} = \dfrac{1}{3}\) và \(MP = 3MN\) nên B, D đúng.
Ngoài ra: \(\dfrac{{NA}}{{PA}} = \dfrac{1}{3}\) \( \Rightarrow \dfrac{{NA}}{{NP}} = \dfrac{{NA}}{{PA - NA}} = \dfrac{1}{{3 - 1}} = \dfrac{1}{2}\) nên A đúng.
Chỉ có C sai.
Hướng dẫn giải:
Sử dụng tính chất đường phân giác ngoài của tam giác:
Định lý: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Chú ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
