Câu hỏi:
2 năm trước
Cho \(\Delta ABC\), trên cạnh \(AB\) lấy điểm \(D\) khác \(A,B\). Qua \(D\) kẻ đường thẳng song song với \(BC\) cắt \(AC\) tại \(E\). Chọn kết luận sai?
Trả lời bởi giáo viên
Đáp án đúng: d
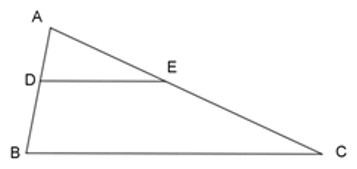
Do \(DE//BC\) nên theo định lý Talet ta có \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) nên C đúng.
Xét \(\Delta ADE\) và \(\Delta ABC\) ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) (cmt)
\(\widehat A\) chung.
\( \Rightarrow \Delta ADE\backsim\Delta ABC\) (c – g – c) nên A đúng
\( \Rightarrow \widehat {ADE} = \widehat {ABC}\) (cặp góc tương ứng) nên D sai.
Hướng dẫn giải:
Nhận xét tính đúng sai của từng đáp án bằng cách xét tam giác đồng dạng và định lý Ta-let.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
