Cho \(\Delta ABC\) có đường cao \(AH,H\) nằm giữa \(BC.\) Biết \(AH = 4,HB = 2,HC = 8.\) Phép đồng dạng \(F\) biến \(\Delta HBA\) thành \(\Delta HAC\). \(F\) được hình thành bởi hai phép biến hình nào?
Trả lời bởi giáo viên
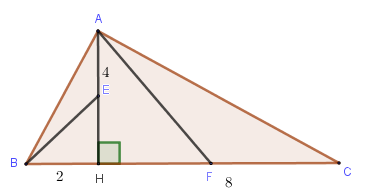
Ta có:
$\begin{array}{l}{Q_{\left( {H, - {{90}^0}} \right)}}\left( B \right) = E;{V_{\left( {H;2} \right)}}\left( E \right) = A\\{Q_{\left( {H, - {{90}^0}} \right)}}\left( A \right) = F;{V_{\left( {H;2} \right)}}\left( F \right) = C\end{array}$
Do đó, nếu ta thực hiện liên tiếp hai phép biến hình là phép quay tâm \(H\) góc quay \( - {90^0}\) và phép vị tự tâm \(H\) tỉ số \(k = 2\) ta sẽ được phép đồng dạng tỉ số \(k = 2\) biến tam giác \(\Delta HBA\) thành tam giác \(\Delta HAC\).
Hướng dẫn giải:
Sử dụng tính chất: Phép đồng dạng là hợp thành của một phép vị tự và phép biến hình.
Lần lượt quan sát các đáp án và kiểm tra.

