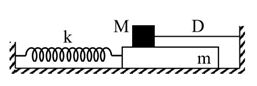
Cho cơ hệ như hình bên. Vật m khối lượng \(100{\rm{ }}g\) có thể chuyển động tịnh tiến, không ma sát trên mặt phẳng nằm ngang dọc theo trục lò xo có \(k{\rm{ }} = {\rm{ }}40{\rm{ }}N/m\). Vật M khối lượng \(300{\rm{ }}g\) có thể trượt trên m với hệ số ma sát \(\mu {\rm{ }} = {\rm{ }}0,2\). Ban đầu, giữ m đứng yên ở vị trí lò xo dãn \(4,5{\rm{ }}cm\) , dây D (mềm, nhẹ, không dãn) song song với trục lò xo. Biết M luôn ở trên m và mặt tiếp xúc giữa hai vật nằm ngang. Lấy \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\) . Thả nhẹ cho m chuyển động. Tính từ lúc thả đến khi lò xo trở về trạng thái có chiều dài tự nhiên lần thứ 3 thì tốc độ trung bình của m là:   

Một hệ gồm hai vật giống nhau có khối lượng \({m_1} = {m_2} = 200g\) dính với nhau bởi một lớp keo mỏng. Một lò xo có chiều dài tự nhiên là \({l_0} = 40cm\), treo thẳng đứng với đầu trên cố định, đầu dưới gắn vào \({m_1}\). Khi hệ vật cân bằng, lò xo dài 44cm. Lấy \(g = 10m/{s^2}\). Nâng hệ vật thẳng đứng đến khi lò xo có chiều dài 38 cm rồi thả nhẹ. Biết \({m_2}\)  khi rời khỏi vật \({m_1}\)  khi lực căng giữa chúng đạt tới 3,5N. Sau khi \({m_2}\)  rời đi, biên độ dao động của vật \({m_1}\)  gắn với giá trị

Một con lắc lò xo nằm ngang gồm vật nặng tích điện \(q = 20{\rm{ }}\mu C\) và lò xo có độ cứng \(k{\rm{ }} = {\rm{ }}10{\rm{ }}N/m\). Khi vật đang nằm cân bằng, cách điện, trên mặt bàn nhẵn thì xuất hiện tức thời một điện trường đều  trong không gian bao quanh có hướng dọc theo trục lò xo. Sau đó con lắc dao động trên một đoạn thẳng dài \(4{\rm{ }}cm\). Độ lớn cường độ điện trường $E$ là:

Một vật nặng có khối lượng m, điện tích \(q{\rm{ }} = {\rm{ }} + {\rm{ }}5.{\rm{ }}{10^{ - 5}}\left( C \right)\) được gắn vào lò xo có độ cứng \(k{\rm{ }} = {\rm{ }}10{\rm{ }}N/m\) tạo thành con lắc lò xo nằm ngang . Điện tích trên vật nặng không thay đổi khi con lắc dao động và bỏ qua mọi ma sát. Kích thích cho con lắc dao động điều hòa với biên độ \(5cm\). Tại thời điểm vật nặng đi qua vị trí cân bằng và có vận tốc hướng ra xa điểm treo lò xo, người ta bật một điện trường đều có cường độ \(E{\rm{ }} = {\rm{ }}{10^4}V/m\), cùng hướng với vận tốc của vật. Khi đó biên độ dao động mới của con lắc lò xo là:

Một vật có khối lượng \(m{\rm{ }} = {\rm{ }}1kg\) được treo vào lò xo có độ cứng \(100N/m\), một đầu lò xo được giữ cố định. Ban đầu vật được đặt ở vị trí lò xo không biến dạng và đặt lên một miếng ván nằm ngang. Sau đó người ta cho miếng ván chuyển động nhanh dần đều thẳng đứng xuống dưới với gia tốc \(a{\rm{ }} = {\rm{ }}2m/{s^2}\). Lấy \(g = {\rm{ }}10m/{s^2}\). Sau khi rời tấm ván vật dao động điều hòa với vận tốc cực đại là :

Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là \({x_1} = {\rm{ }}10cos(2\pi t + {\rm{ }}\varphi )cm\) và \({x_2} = {\rm{ }}{A_2}cos(2\pi t - \dfrac{\pi }{2})cm\) thì dao động tổng hợp là \(x = Acos(2\pi t - \dfrac{\pi }{3})cm\) . Khi năng lượng dao động của vật cực đại thì biên độ dao động \({A_2}\) có giá trị là:

Một con lắc lò xo ngang có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\) nặng \(200g\). Bỏ qua ma sát giữa vật và mặt phẳng ngang. Khi vật đang ở vị trí cân bằng thì tác dụng vào vật một lực không đổi \(2N\) theo dọc trục của lò xo. Tốc độ của vật sau \(\dfrac{2}{{15}}s\)  có giá trị là bao nhiêu? Lấy ${\pi ^2} = 10$

Con lắc lò xo gồm lò xo có độ cứng \(200N/m\) , quả cầu $m$ có khối lượng \(1kg\) đang dao động điều hòa theo phương thẳng đứng với biên độ \(12,5cm\). Khi quả cầu xuống đến vị trí thấp nhất thì có một vật nhỏ khối lượng \(500g\) bay theo phương trục lò xo, từ dưới lên với tốc độ \(6m/s\) tới dính chặt vào M. Lấy \(g{\rm{ }} = {\rm{ }}10m/{s^2}\). Sau va chạm , hai vật dao động điều hòa. Biên độ dao động của hệ hai vật sau va chạm là :