Câu hỏi:
2 năm trước
Một hệ gồm hai vật giống nhau có khối lượng \({m_1} = {m_2} = 200g\) dính với nhau bởi một lớp keo mỏng. Một lò xo có chiều dài tự nhiên là \({l_0} = 40cm\), treo thẳng đứng với đầu trên cố định, đầu dưới gắn vào \({m_1}\). Khi hệ vật cân bằng, lò xo dài 44cm. Lấy \(g = 10m/{s^2}\). Nâng hệ vật thẳng đứng đến khi lò xo có chiều dài 38 cm rồi thả nhẹ. Biết \({m_2}\) khi rời khỏi vật \({m_1}\) khi lực căng giữa chúng đạt tới 3,5N. Sau khi \({m_2}\) rời đi, biên độ dao động của vật \({m_1}\) gắn với giá trị
Trả lời bởi giáo viên
Đáp án đúng: c
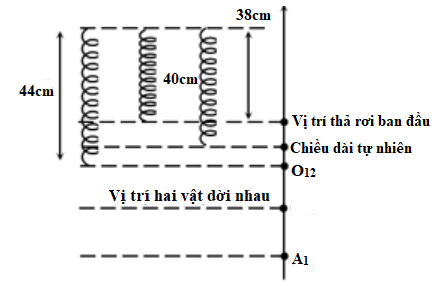
+ Hệ vật \(\left( {{m_1} + {m_2}} \right)\) dao động với:
\(\left\{ \begin{array}{l}\Delta {l_0} = 44 - 40 = 4cm\\A = 2 + 4 = 6cm\\\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{g}{{\Delta {l_{012}}}}} = \sqrt {\frac{{10}}{{0,04}}} = 5\pi \,rad/s\end{array} \right.\)
\( \Rightarrow k = \frac{{mg}}{{\Delta {l_{012}}}} = \frac{{0,4.10}}{{0,04}} = 100N/m\)
+ Áp dụng định luật II Niuton cho \({m_2}\) tại vị trí hai vật tách nhau:
\(\begin{array}{l}\overrightarrow {{P_2}} + \overrightarrow {{F_{12}}} = {m_2}\overrightarrow a \Leftrightarrow - {m_2}g + {F_{12}} = {m_2}a\\ \Leftrightarrow - {m_2}g + {F_{12}} = {m_2}.{\omega ^2}.\left| x \right|\\ \Leftrightarrow - 0,2.10 + 3,5 = 0,2.{\left( {5\pi } \right)^2}.\left| x \right| \Rightarrow \left| x \right| = 3cm\end{array}\)
\( \Rightarrow {v_{12}} = \omega \sqrt {{A^2} - {x^2}} = 5\pi \sqrt {{6^2} - {3^2}} = 81,6cm/s\)
+ Sau khi \({m_2}\) dời khỏi vật \({m_1}\) \( \Rightarrow {m_1}\) dao động điều hòa quanh vị trí cân bằng mới với:
\(\Delta {l_{01}} = \frac{{{m_1}g}}{k} = \frac{{0,2.10}}{{100}} = 0,02m = 2cm\)
\({\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,2}}} = 10\sqrt 5 rad/s\)
Tại vị trí \({m_2}\) hai vật tách nhau có:
\(\left\{ \begin{array}{l}
{x_1} = 2 + 3 = 5cm\\
{v_1} = {v_{12}} = 81,6cm/s
\end{array} \right.\)
\( \Rightarrow {A_1} = \sqrt {x_1^2 + \frac{{v_1^2}}{{\omega _1^2}}} = \sqrt {{5^2} + {{\left( {\frac{{81,6}}{{10\sqrt 5 }}} \right)}^2}} = 6,2cm\)
Hướng dẫn giải:
+ Độ biến dạng tại VTCB: \(\Delta l = \frac{{mg}}{k}\)
+ Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta l}}} \)
+ Công thức tính vận tốc: \(v = \pm \omega \sqrt {{A^2} - {x^2}} \)
+ Biên độ dao động: \(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} \)
+ Áp dụng biểu thức định luật II Niuton cho vật \({m_2}\) tại vị trí hai vật rời nhau.
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
