Cho các số phức \({z_1}\), \({z_2}\), \({z_3}\) thỏa mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1\). Tính giá trị lớn nhất của biểu thức \(P = {\left| {{z_1} - {z_2}} \right|^2} + {\left| {{z_2} - {z_3}} \right|^2} + {\left| {{z_3} - {z_1}} \right|^2}\).

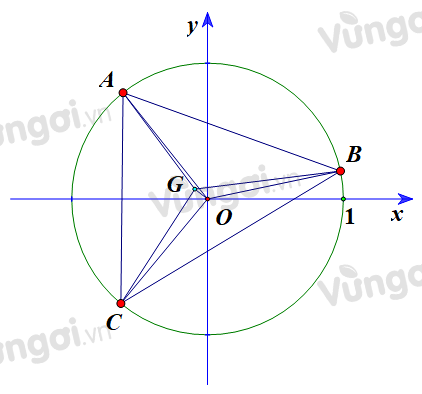
Gọi \(A\left( {{x_1}\,;{y_1}} \right)\), \(B\left( {{x_2}\,;{y_2}} \right)\), \(C\left( {{x_3}\,;{y_3}} \right)\) là các điểm lần lượt biễu diễn các số phức \({z_1}\), \({z_2}\), \({z_3}\).

Vì \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right|\) nên \(A\); \(B\); \(C\) thuộc đường tròn tâm \(O\) bán kính bằng 1.

\(\left| {{z_1} - {z_2}} \right| = AB\); \(\left| {{z_2} - {z_3}} \right| = BC\); \(\left| {{z_3} - {z_1}} \right| = AC\).

\(P = {\left| {{z_1} - {z_2}} \right|^2} + {\left| {{z_2} - {z_3}} \right|^2} + {\left| {{z_3} - {z_1}} \right|^2}\)\( = A{B^2} + B{C^2} + A{C^2}\)\( = {\left( {\overrightarrow {OB}  - \overrightarrow {OA} } \right)^2} + {\left( {\overrightarrow {OC}  - \overrightarrow {OB} } \right)^2} + {\left( {\overrightarrow {OA}  - \overrightarrow {OC} } \right)^2}\)\( = 6 - 2\left( {\overrightarrow {OA} .\overrightarrow {OB}  + \overrightarrow {OB} .\overrightarrow {OC}  + \overrightarrow {OA} .\overrightarrow {OC} } \right)\).

Mặt khác \({\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} } \right)^2} = O{A^2} + O{B^2} + O{C^2} + 2\left( {\overrightarrow {OA} .\overrightarrow {OB}  + \overrightarrow {OB} .\overrightarrow {OC}  + \overrightarrow {OA} .\overrightarrow {OC} } \right)\).

\(P = 9 - {\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} } \right)^2}\)\( = 9 - {\left( {3\overrightarrow {OG} } \right)^2}\)\( = 9 - 9O{G^2} \le 9\) (với \(G\) là trọng tâm tam giác\(ABC\)).

Đẳng thức xảy ra khi \(G \equiv O\), hay \(\Delta ABC\) đều.