Cho các đường tròn \(\left( {A;10\,{\rm{cm}}} \right),{\rm{ }}\left( {B;15\,{\rm{cm}}} \right),{\rm{ }}\left( {C;15\,cm} \right)\)  tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại \(A'\). Đường tròn \(\left( A \right)\)  tiếp xúc với đường tròn \(\left( B \right)\) và \(\left( C \right)\) lần lượt tại \(C'\)  và \(B'.\)

Tính diện tích tam giác \(A'B'C'.\)

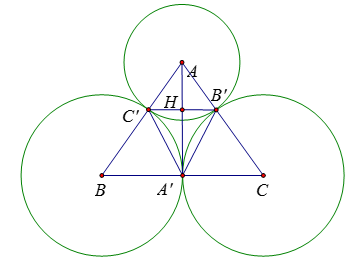
Ta có: \(\dfrac{{AC'}}{{AB}} = \dfrac{{AB'}}{{AC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5}\) 

\( \Rightarrow B'C'{\rm{ }}//{\rm{ }}BC\)  do đó  \(B'C' \bot AA'\)

Lại có: \(\dfrac{{B'C'}}{{BC}} = \dfrac{{AC'}}{{AB}} \Rightarrow \dfrac{{B'C'}}{{30}} = \dfrac{2}{5} \Leftrightarrow B'C' = 12\,cm\)

 Xét \(\Delta ABA'\)  có \(B'C'{\rm{ }}//{\rm{ }}BC\) nên theo định lý Ta-let ta có \(\dfrac{{AH}}{{A'A}} = \dfrac{{BC'}}{{BA}} \Rightarrow \dfrac{{AH}}{{20}} = \dfrac{{15}}{{25}} \Rightarrow AH = 12\,cm\) (do theo câu trước thì \(AA' = 20\,cm\) )

Diện tích tam giác \(A'B'C'\) là: \(S = \dfrac{1}{2}B'C'.AH = \dfrac{1}{2}.12.12 = 72\,\left( {c{m^2}} \right)\)