Cho các đường tròn \(\left( {A;10\,{\rm{cm}}} \right),{\rm{ }}\left( {B;15\,{\rm{cm}}} \right),{\rm{ }}\left( {C;15\,cm} \right)\)  tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại \(A'\). Đường tròn \(\left( A \right)\)  tiếp xúc với đường tròn \(\left( B \right)\) và \(\left( C \right)\) lần lượt tại \(C'\)  và \(B'.\)

Chọn câu đúng nhất.

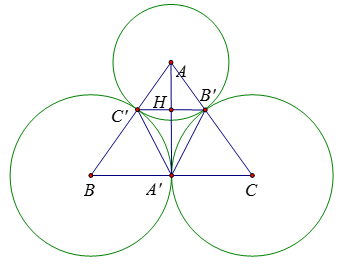
 +) Theo tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài ta có:

\(AB = BC' + C'A = 25\,cm;{\rm{ }}AC = AB' + B'C = 25\,cm;\) \({\rm{ }}BC = BA' + A'C = 30cm\) và \(A'\)  là trung điểm của \(BC\) (vì \(A'B = A'C = 15cm\))

\(\Delta ABC\) cân tại \(A\)  có \(AA'\)  là đường trung tuyến nên cũng là đường cao

\( \Rightarrow AA' \bot BC\)

\( \Rightarrow AA'\) là tiếp tuyến chung của hai đường tròn (B) và (C)

Xét tam giác \(AA'C\)  vuông tại \(A'\)  có:

\(\;A'{A^2}\; = {\rm{ }}A{C^2}\; - {\rm{ }}A'{C^2}\; = {\rm{ }}{25^2} - {\rm{ }}{15^2}\; = 400\)\( \Rightarrow A'A{\rm{ }} = {\rm{ }}20\,cm\)