Cho bát diện đều có độ dài cạnh bằng \(a\). Tính tỉ số giữa thể tích khối cầu nội tiếp và thể tích khối cầu ngoại tiếp hình bát diện đều đã cho.
Trả lời bởi giáo viên
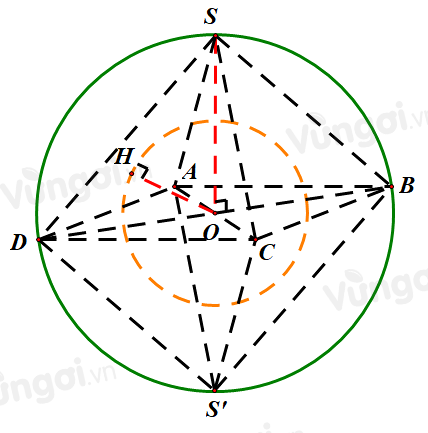
Gọi cạnh bát diện đều là a; bát diện đều có các mặt chéo là hình vuông khi đó độ dài các đường chéo
\(AC = BD = SS' = a\sqrt 2 \)
Mặt cầu nội tiếp và ngoại tiếp đều có tâm O, khi đó bán kính mặt cầu ngoại tiếp là \(R = OA = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\)
Bán kính mặt cầu nội tiếp là khoảng cách từ O đến các mặt bên.
Ta có hình chóp O.SAD là hình chóp có OA,OS,OD đôi một vuông góc với nhau với H là hình chiếu của O lên SAD thì có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{D^2}}} + \dfrac{1}{{O{A^2}}} = \dfrac{3}{{{R^2}}}\)
\( \Rightarrow r = OH = \dfrac{{a\sqrt 6 }}{6}\)
Có \(\dfrac{r}{R} = \dfrac{1}{{\sqrt 3 }}\)
Khi đó có tỷ số thể tích khối cầu nội tiếp cho khối cầu ngoại tiếp là \({\left( {\dfrac{r}{R}} \right)^3} = {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^3} = \dfrac{1}{{3\sqrt 3 }}\)
Hướng dẫn giải:
- Gọi cạnh bát diện đều là a
- Biểu diễn bán kính r và R theo a.
- Lập tỷ số thể tích.
- O.SAD là hình chóp có OA,OS,OD đôi một vuông góc với nhau với H là hình chiếu của O lên SAD thì có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{D^2}}} + \dfrac{1}{{O{A^2}}}\)
Câu hỏi khác
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 1, có đáp án và lời giải chi tiết
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 2, có đáp án và lời giải chi tiết
- Đề thi chính thức ĐGTD Bách khoa 2022 - mã 103 có đáp án và lời giải chi tiết
- Đề thi thử ĐGTD Bách khoa trường Yên Lạc - Lần 2 có đáp án và lời giải chi tiết
