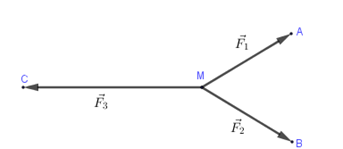
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều bằng \(100N\) và $\widehat {AMB} = {60^0}$. Khi đó cường độ lực của $\overrightarrow {{F_3}} $ là:
Trả lời bởi giáo viên
Vật \(M\) đứng yên \( \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
Hay \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
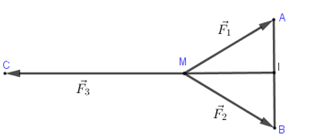
Gọi \(I\) là trung điểm của \(AB\) \( \Rightarrow 2\overrightarrow {MI} + \overrightarrow {MC} = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {MC} = - 2\overrightarrow {MI} \Rightarrow MC = 2MI\)
Gọi \(I\) là trung điểm của \(AB.\)
Vì \(MAB\) là tam giác đều nên \(MI = MA.\dfrac{{\sqrt 3 }}{2} = 50\sqrt 3 .\)
Vậy \(MC = 2MI = 100\sqrt 3 N\)
Vậy: \(\overrightarrow {{F_3}} \) có cường độ \(100\sqrt 3 \,N\).
Hướng dẫn giải:
- Sử dụng phương pháp tổng hợp lực để tính \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).
- Vật \(M\) đứng yên \( \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right|\).

